¿Qué es una fracción? Esta pregunta no es fácil de contestar, a pesar de ser un elemento tan familiar para todos, las fracciones tienen múltiples significados que hacen difícil su definición y, por tanto, su didáctica y su comprensión.
Esos dos números que colocamos uno sobre el otro y separamos con una línea horizontal se pueden interpretar de hasta cinco formas diferentes, las cuales veremos en este post, junto con algunas de sus vinculaciones didácticas.
1. Relación entre la Parte y el Todo
Es la interpretación más sencilla y evidente para los niños, es el uso de la fracción para referirnos a una parte de la unidad, del todo:

Es una interpretación muy común y por la cual se suelen empezar las secuencias didácticas pero plantea un problema a la hora de introducir las fracciones impropias; “¿cómo voy a coger más partes de las que hay?”. Pero, al mismo tiempo es muy representativa, se relaciona mucho con elementos y situaciones de la vida real, cercanas a los niños, lo cual permite una fácil modelización, muy importante en los primeros niveles de una secuencia didáctica para la comprensión de lo que se está haciendo y representando.
2. Puntos en la Recta Numérica
En relación a la didáctica de las fracciones impropias, la continuidad de la recta numérica se presenta como un recurso muy útil; “ahora sí que puedo coger más, porque después del 1 viene el 2, luego el 3… y así ¡hasta el infinito!”.
Veamos un ejemplo, ¿qué esto de una fracción como un punto en la recta numérica?
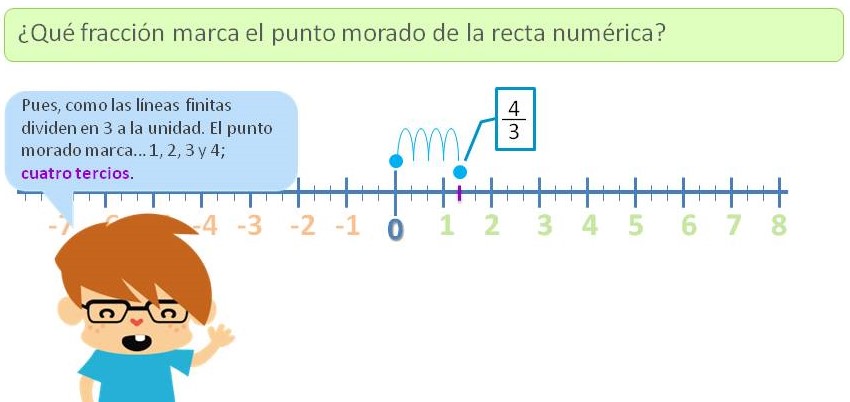
Si esto te ha resultado interesante, seguro que te gusta el post en el que hablamos sobre cómo ubicar números en la recta numérica
3. Operador
Cuando comenzamos a operar con fracciones, sobre todo al multiplicar (operación de muy difícil didáctica, ya que “veces más” hace el número “más pequeño”), se entiende como un operador, elemento que, al aplicarlo sobre el número, afecta a su valor; de tal modo, “si yo aplico ½ a 6, 6 pasa a ser 3”. Esto ocurre en niveles muy básicos de comprensión, cuando aún no se logra comprender ½ de 6 como ½ X 6 y, menos todavía, la fracción como una división. Es, en cierto modo, una comprensión de las mismas como lo que en el futuro los niños estudiarán como funciones:
|
Al aplicar ½… |
…sobre 6… | …me da 3. |
| F(x)= ½ x | x = 6 |
F(x) = 3 |
4. Razón
Consiste en la comprensión de las fracciones como la expresión de una relación entre cantidades. Se refiere a la comprensión de la fracción como la expresión numérica de: “Por cada x hay y”.
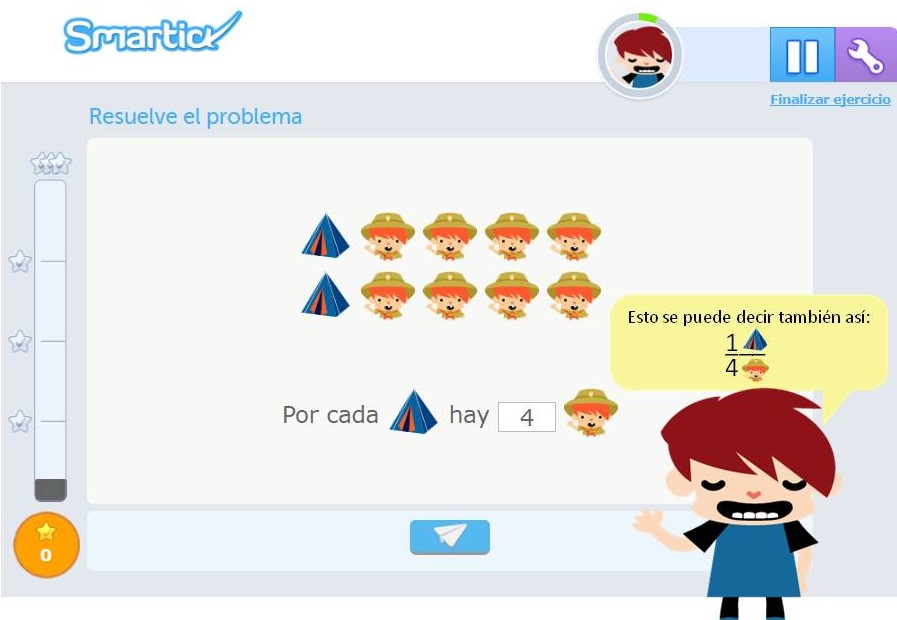
Además, esta interpretación del concepto de fracción, permite la introducción al concepto de escalas: “Cada cm que mido en el plano hay 1000 cm en la realidad”.
5. Cociente
La interpretación de la fracción como un cociente supone la mayor dificultad de comprensión y se trata de la analogía entre divisiones y fracciones. Dificultad que reside en el hecho de que las fracciones son concebidas como números, mientras que las divisiones son una operación.
Así, las diferentes interpretaciones han sido presentadas en orden de dificultad, lo cual es importante tener en cuenta a la hora de introducirlas; teniendo en cuenta que la tendencia general en la dificultad de los contenidos matemáticos es de lo contextualizado a lo abstracto, de lo concreto a lo general:
|
Número contextualizado |
Número como entidad abstracta | Número con una función |
| 1/3 de pizza | 1/3 |
f(x)=1/3 x |
Si te ha gustado este post, puedes encontrar más información sobre el trabajo con fracciones en:
- Barras de Singapur y fracciones. Presentan las barras de Singapur como material didáctico para la comprensión y trabajo con fracciones:
- Estimaciones de fracciones
- Convertir fracciones en números decimales
- Y muchos otros posts en el Blog de Smartick
Además en Smartick podrás aprender fracciones y un montón de conceptos básicos de matemáticas, trabajando con ejercicios adaptados al alumno en tiempo real. ¡¡Pruébalo GRATIS!!
Para seguir aprendiendo:
- Barras de Singapur aplicadas a la suma de fracciones
- Cómo representar fracciones en la recta numérica
- Fracción: aprende todo sobre fracciones
- Ubicar los diferentes números en la recta numérica
- Uso de la recta numérica para comparar fracciones
- Number talks: aprende matemáticas hablando - 31/05/2023
- Estrategias de cálculo mental para niños - 25/03/2021
- Ecuaciones reducibles: ¿qué son? ¿cómo se resuelven? - 03/02/2020








muy chevere estas definiciones
Gracias por el aporte de las diferentes definiciones y conceptualizaciones de lo que es la fracción.
como se saca la equivalencia de una fraccion
Hola Paola:
Estos posts del blog de Smartick seguro que te ayudan a entender las fracciones equivalentes:
https://www.smartick.es/blog/matematicas/recursos-didacticos/fracciones-equivalentes/
https://www.smartick.es/blog/matematicas/recursos-didacticos/fracciones-equivalentes-2/
https://www.smartick.es/blog/matematicas/recursos-didacticos/ejemplos-de-fracciones-equivalentes/
https://www.smartick.es/blog/matematicas/recursos-didacticos/ejercicios-con-fracciones-equivalentes/
En el blog de Smartick hay una lupa en la que puedes buscar los temas en que te interese profundizar.
Un saludo!
que es una fraccion equivalente
Hola Mariano:
En el blog de Smartick tenemos un montón de entradas explicando qué es una fracción equivalente:
https://www.smartick.es/blog/matematicas/recursos-didacticos/fracciones-equivalentes/
https://www.smartick.es/blog/matematicas/recursos-didacticos/fracciones-equivalentes-2/
Y entradas con ejercicios y ejemplos:
https://www.smartick.es/blog/matematicas/recursos-didacticos/ejercicios-con-fracciones-equivalentes/
https://www.smartick.es/blog/matematicas/recursos-didacticos/ejemplos-de-fracciones-equivalentes/
https://www.smartick.es/blog/matematicas/recursos-didacticos/sumas-de-fracciones/
https://www.smartick.es/blog/matematicas/recursos-didacticos/un-medio-tercio-cuarto/
Un saludo!