En otros posts anteriores hemos hablado de cómo aplicar el Método Singapur a las diferentes operaciones matemáticas. En el de hoy vamos a ver qué ventajas tiene el uso de este método para la resolución de problemas.
Sabemos que la resolución de problemas es una de las partes de las matemáticas más importantes y hay que proporcionar a los estudiantes herramientas que faciliten el aprendizaje y la comprensión de los conceptos matemáticos. Una forma de mejorar la capacidad de los estudiantes en la resolución de problemas es ayudarles en la visualización representativa de éstos. El Método Singapur se utiliza para representar y resolver problemas de estructuras complejas, dibujando un modelo pictórico que permite procesar la información dada y dar sentido a las cantidades conocidas, desconocidas y las relaciones entre ellas.
Este método ayuda a los estudiantes a obtener una mejor comprensión de los conceptos matemáticos, planear los pasos para la resolución de problemas y resulta menos abstracto que el método algebraico. Todo esto puede generar una mayor motivación para resolver problemas más difíciles.
Vamos a ver unos cuantos ejemplos aplicando las Barras de Singapur para la resolución de problemas

María va a celebrar su cumpleaños en casa y ha invitado a 20 compañeros de clase. Sabemos que 3/5 son chicas y el resto chicos. ¿A cuántas chicas ha invitado María a su fiesta?
- Lo primero que hacemos es dibujar una barra que represente el total de compañeros invitados a la fiesta:
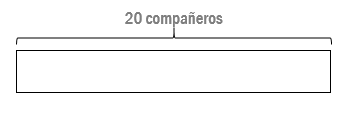
- Después, como el enunciado nos dice que 3/5 partes de los invitados son chicas, dividimos la barra en 5 partes:
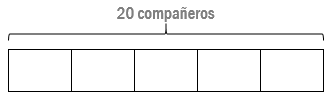
- Y coloreamos la parte de la barra a la que se refiere a la cantidad de chicas, 3/5:
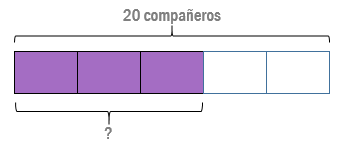
- Una vez tenemos el problema planteado gráficamente, podemos buscar la mejor manera de resolverlo. Sabemos que el total de invitados a la fiesta son 20 compañeros, que hemos representado con la primera barra y este total lo hemos dividido en 5 partes. Ahora podemos descubrir cuántos compañeros representar una parte de ese todo:
5 partes = 20 compañeros
1 parte = 20 ÷ 5 = 4 compañeros en cada parte
3 partes = 4 x 3 = 12 chicas que ha invitado María a su fiesta de cumpleaños
El resto son chicos= 20 total de invitados – 12 chicas= 8 chicos ha invitado María a su cumpleaños

Guillermo tiene 130 coches de colección en total. Tiene 4 veces más coches convertibles que los que no son convertibles. ¿Cuántos coches convertibles tiene Guillermo?
- Dibujamos una barra para los coches convertibles y la dividimos en 4 partes, ya que el enunciado nos dice que Guillermo tiene 4 veces más coches convertibles que no convertibles:
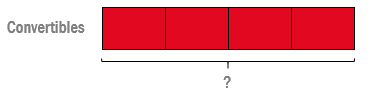
- Ahora que ya tenemos representada la cantidad de coches convertibles que tiene Guillermo podemos representar la parte de coches no convertibles. Sabiendo que los convertibles son 4 veces más que los no convertibles, debemos dibujar una barra con las dimensiones de una de las partes del total de los convertibles:
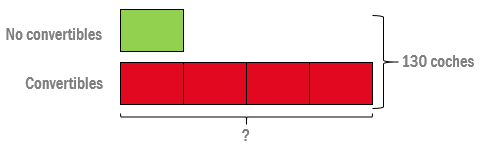
- Teniendo todas las representaciones, ya podemos resolver el problema:
El total de todas las partes es 130 coches, es decir que 5 partes = 130 coches
1 parte = 130 ÷ 5 = 26 coches
4 partes = 26 x 4 = 104 coches convertibles
Hasta aquí unos ejemplos de la aplicación de las Barras de Singapur a la resolución de problemas, otro día seguimos con más ejemplos.
Si quieres seguir aprendiendo matemáticas, regístrate en Smartick para disfrutar de la prueba gratuita.
Para seguir aprendiendo:
- Barras de Singapur aplicadas a las fracciones
- Barras de Singapur aplicadas a la resolución de problemas II
- Barras de Singapur aplicadas al concepto de porcentaje
- Cómo resolver problemas de restas
- Ejercicios de divisiones resueltos con el método Singapur
- Barras de Singapur aplicadas al concepto de porcentaje - 07/08/2017
- Geometría y figuras planas con la ayuda del Tangram - 10/07/2017
- Qué es una división. Conceptos basicos - 12/06/2017








en el problema: Guillermo tiene 130 coches de colección en total. Tiene 4 veces más coches convertibles que los que no son convertibles. ¿Cuántos coches convertibles tiene Guillermo?
está mal solucionado debido a que dice que tiene 4 veces más coches convertibles que no convertibles, no que la cantidad de convertibles es 4 veces la de no convertibles
Hola Gilberto:
Muchas gracias por tu comentario. El problema no está mal solucionado. Si multiplicas 26 (cantidad de coches no convertibles) por 4, el resultado es 104. Justo 104, 4 veces 26 (coches no convertibles), son los coches convertibles. Decir que hay 4 veces más coches convertibles que no convertibles, es lo mismo que decir que la cantidad de convertibles es 4 veces la de no convertibles.
Gilberto no es lo mismo:
Si ganas 1000 euros y te ofrecen pagarte 4 veces más que tu sueldo actual, Cuánto deberán pagarte ?
Respuesta:
1.000 + 4 veces 1.000 = 5.000 euros.
Hola Claudio:
Gracias por tu comentario. En castellano utilizamos los numerales multiplicativos como el doble, el triple… para referirnos a 2 veces más, 3 veces más… Cuando decimos 4 veces más que x nos referimos a 4x, exactamente igual que si dijéramos el cuádruple. La partícula «más» no tiene significado de suma sino de que la comparación es de aumento. Si en el caso de una comparación de disminución dijésemos «cuatro veces menos» nos referiríamos a la cuarta parte.
¡Un saludo!
excelente forma de resolver problemas matemáticos.
Veo muy interesante este modelo me recuerda mucho al utilizado por Isabel Echenique en su libro la resolución de problemas en primaria.
veo muy practicas las barras de singapur para resover el prblema de forma grafica, esta forma piensa aplicarla a la resolución de problemas con mis nietos de forma que los comprendan mediante la visualización
estan en 6º