En este blog hemos escrito ya muchas entradas sobre fracciones. Hace poco, uno de nuestros lectores nos hacía una consulta sobre el contenido de este post de clasificación de fracciones: «Perdone pero no entiendo las fracciones impropias… pienso que es imposible tomar 11 partes de algo que está dividido en 8».
Cuando utilizamos y aprendemos las fracciones (o cualquier otro tema de las matemáticas) hay que tener algo muy presente: las matemáticas son una disciplina muy concreta que se utiliza para explicar o representar casi cualquier suceso de nuestro entorno. En estos posts puedes ver algunos ejemplos de a qué me refiero:
- Ubicar los diferentes números en la recta numérica
- Estadística: ¿qué es y para qué sirve?
- Ángulo – agudo, obtuso, llano y recto
- Curiosidades de algunas figuras geométricas
Por eso, muchos aspectos de las matemáticas se pueden entender de diferentes formas. Ese es el caso de las fracciones. Nuestro lector solamente las entendía como la relación de la parte con el todo («es imposible tomar 11 partes de algo que está dividido en 8»), pero se pueden entender de más maneras.
Aquí explicamos tres diferentes formas de entender las fracciones:
1. Fracciones como la relación parte-todo:
Es de los primeros usos que aprendemos de las fracciones, como una forma de expresar una relación entre la parte que tenemos con el todo de donde lo hemos tomado.
Por ejemplo, me tomé un octavo de tarta: Significa que de toda la tarta, que estaba partida en 8 trozos iguales, solo tomé 1 trozo.
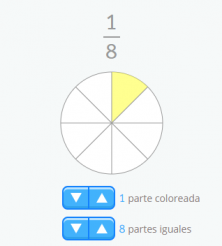
2. Fracciones como relación entre diferentes elementos:
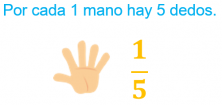
Por otro lado, las fracciones se pueden utilizar para explicar la relación que existe entre un objeto y otro diferente, cuando existe una relación constante. Por ejemplo, la relación que existe entre las manos y los dedos de las manos es 1/5, porque por cada mano hay 5 dedos.
 3. Fracciones como números que podemos representar como puntos de la recta numérica:
3. Fracciones como números que podemos representar como puntos de la recta numérica:
Pero las fracciones también son números que podemos representar en la recta numérica, cambiando la idea anterior de “todo” por “unidad”. Ésta será la que dividiremos en tantas partes iguales como indique el denominador y el numerador indicará el punto concreto en la recta numérica.
Vamos a ver dos ejemplos:
- Fracción propia: es menor que la unidad:
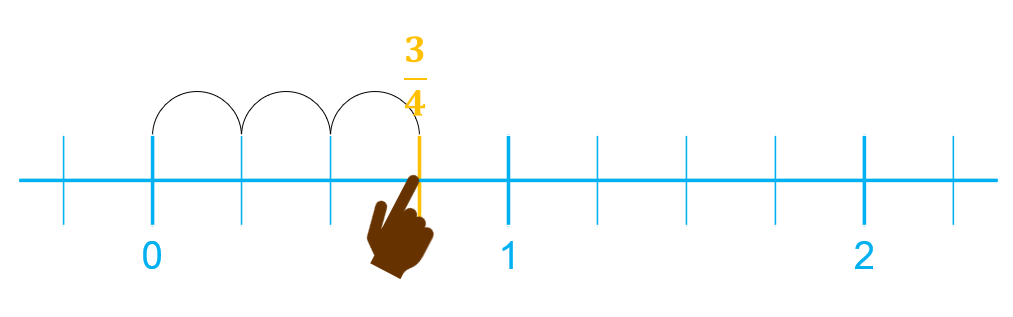
- Fracción impropia: es mayor que la unidad:
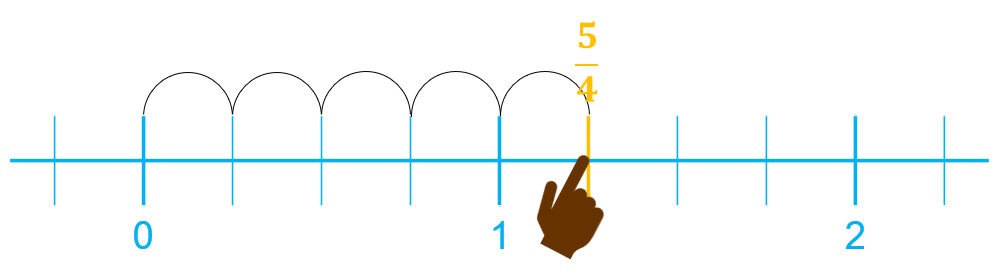
Por eso, a veces podremos tomar once octavos de una tarta, porque el denominador nos está indicando el número de partes iguales en que está dividida la unidad, no el “todo” o total de tarta que teníamos… ¡problema resuelto!

Si quieres seguir aprendiendo sobre las diferentes formas de utilizar las fracciones, ¡entra en Smartick! y pruébalo gratis.
Para seguir aprendiendo:
- Cómo representar fracciones en la recta numérica
- Uso de la recta numérica para comparar fracciones
- Fracción: aprende todo sobre fracciones
- Ubicar los diferentes números en la recta numérica
- Introducción a las fracciones
- Number talks: aprende matemáticas hablando - 31/05/2023
- Estrategias de cálculo mental para niños - 25/03/2021
- Ecuaciones reducibles: ¿qué son? ¿cómo se resuelven? - 03/02/2020








Me sirvió mucho, muchas gracias. Saludos desde secundaria.
Excelente recursos para aprender y enseñar