Explicación de la fórmula para calcular el mínimo común múltiplo

“Para calcular el mínimo común múltiplo cogemos los factores no comunes y comunes con mayor exponente”

Seguro que a muchos os suena esta frase, pero ¿qué quiere decir? ¿por qué todos los factores y, de los comunes, los que tienen mayor exponente? ¡Vamos a descubrirlo!

El mínimo común múltiplo es el menor múltiplo común a dos o más números, como explicábamos en el post: ¿Qué es el mcm?

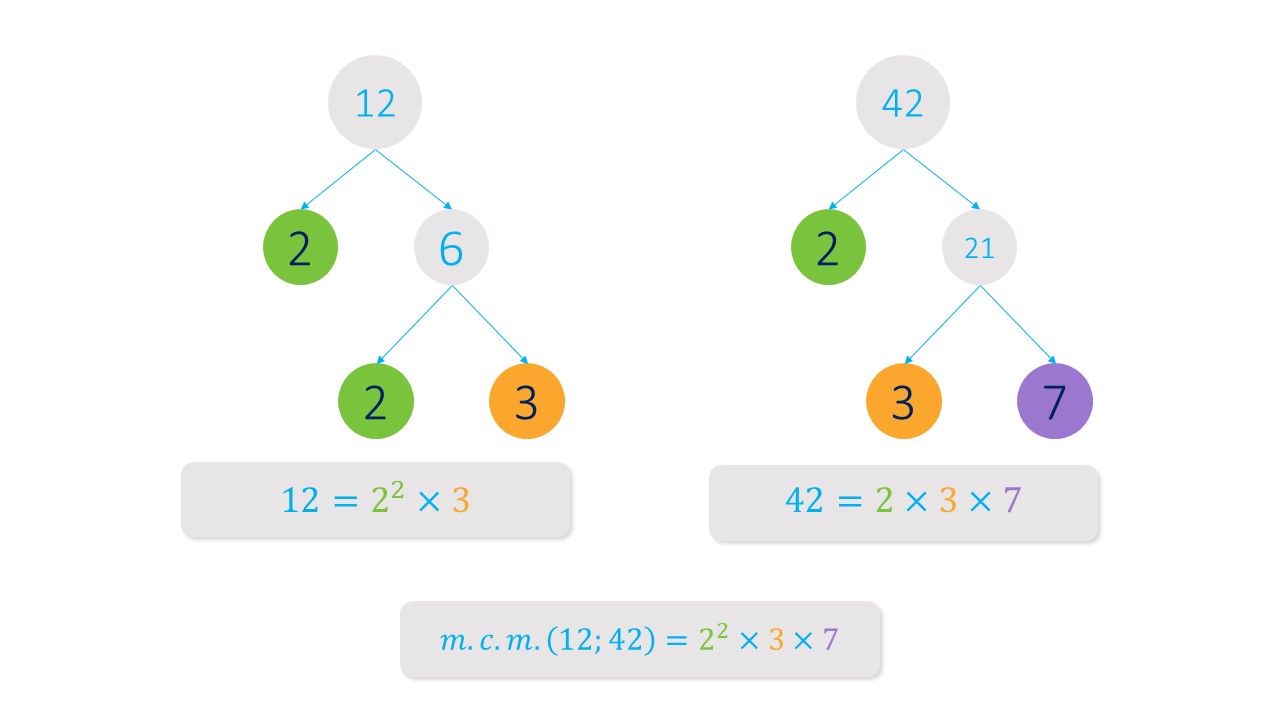
Bien, ahora analicemos otra elemento muy importante de nuestra investigación: la factorización en números primos de un número. Todos los números tienen una factorización única en números primos, es como el DNI de los números.

Por ejemplo: el "DNI" del 12 es 2^2·3, el del 42 es 2·3·7.

Pues vamos a utilizar estos dos números como ejemplo para descubrir las razones de esa frase con la que hemos abierto el post.

Cuando calculamos el mínimo común múltiplo de dos números (en este caso), estamos buscando el menor múltiplo que sea, a la vez, múltiplo de ambos números.

En este caso será el mínimo común múltiplo de 12 y 42 [m.c.m.(12; 42)] será igual a 12 por x o 42 por y:

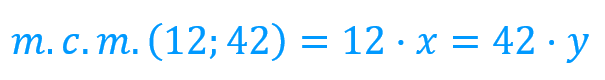
Como hemos dicho que la factorización del 12 es 2^2·3. Podemos decir que:

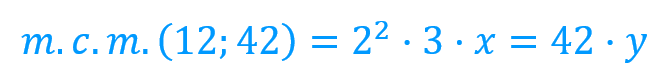Como hemos dicho que la factorización del 42 es 2·3·7. Podemos decir que:

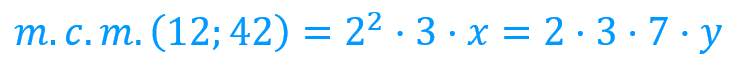Perfecto, ahora veamos, vamos a fijarnos solo en esta parte de la expresión:

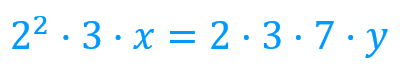
Necesitamos, en ambos lados, los mismos factores primos, porque estamos buscando el mismo número, que vamos a escribir según su factorización en números primos.

Vemos que la factorización de este número tendrá un 3, que está en los dos términos de la expresión, un 2 al cuadrado, que solo está en el término de la izquierda, así que sabemos que la y será un 2.

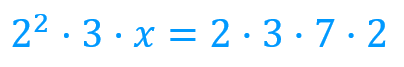
Si nos fijamos en el término de la derecha vemos que “ese número”, el mínimo común múltiplo de 12 y 42, tendrá también el 7 como factor, que no aparece en el término de la izquierda. Así sabemos que la x es un 7, obteniendo:

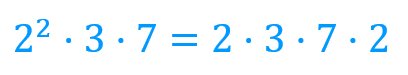
Si agrupamos en potencias los factores comunes, obtenemos la misma expresión a ambos lados de la expresión:

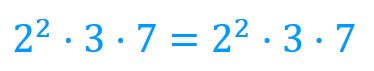
Es decir, el mínimo común múltiplo de 12 y 42 es 84:

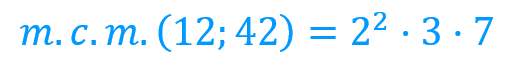
Estos factores son todos los que no tienen en común el 12 y el 42, es decir, el 7, y de los comunes, el que mayor exponente tiene. Los factores comunes son el 2 y el 3, el 3 tiene exponente 1 en ambos casos pero, entre los “doses” elegimos el de mayor exponente, 2 al cuadrado.

¿Qué te ha parecido? ¿Ya lo sabías?

Si quieres seguir aprendiendo cosas como esta, entra en Smartick y pruébalo gratis.

Para seguir aprendiendo:

• ¿Qué es el mínimo común múltiplo (mcm)?
• Números primos: actividades en Smartick
• MCD o Máximo Común Divisor
• Máximo común divisor (MCD): qué es, características y cómo calcularlo
• Para qué sirve la descomposición factorial

Refuerza las matemáticas con 15 minutos al día

Refuerza las matemáticas con 15 minutos al día

Smartick es el aliado perfecto para dominar las matemáticas de manera divertida

Prueba GRATIS 7 días

• Acerca de
• Últimas entradas

Susana Molina

Susana es graduada en Magisterio de Primaria por la Universidad Autónoma de Madrid y tiene un máster en Atención de las Necesidades Educativas Especiales en Educación Infantil y Primaria por la Universidad Rey Juan Carlos.
Forma parte del equipo de desarrollo de contenidos de Smartick, donde se encarga de elaborar secuencias didácticas, ejercicios y tutoriales. También colabora en la atención de sugerencias de los alumnos en "El Pozo".
Cree en la educación como motor de desarrollo de la sociedad y en el conocimiento como clave esencial para el crecimiento individual.
Sus pasiones son la educación en todas sus modalidades, montar en bici, el senderismo y escaparse de acampada siempre que puede.

Últimas entradas de Susana Molina (ver todo)

• Number talks: Aprende matemáticas hablando - 31/05/2023
• Estrategias de cálculo mental para niños - 25/03/2021
• Ecuaciones reducibles: ¿qué son? ¿cómo se resuelven? - 03/02/2020