En entradas anteriores hemos aprendido a multiplicar un número decimal por 10.
Hoy vamos a entender mejor la multiplicación de números decimales utilizando un material manipulativo que es de uso muy común: el dinero. Va a ayudarnos a comprender por qué al multiplicar un número decimal por 10 se mueve la coma del numero decimal un posición a la derecha.
Equivalencia de los billetes o monedas con los números
Primero, vamos a establecer la equivalencia de cada moneda o billete con su escritura simbólica, con el número correspondiente.
Los euros son números enteros y los céntimos números decimales. Por ejemplo:

De esta manera, si tenemos:
- 3 billetes de 10 euros
- 5 monedas de 1 euro
- 3 monedas de 10 céntimos
- y 7 monedas de 1 céntimo…

Hay un total de 35 euros y 37 céntimos. O lo que es lo mismo, el número 35,37
Multiplicar cualquier moneda por 10
Para multiplicar una moneda o billete por 10 sólo es necesario repetirla 10 veces.

10 billetes de 10 euros tienen el mismo valor que un billete de 100 euros.
![]()
Entonces,
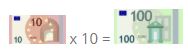
Ahora, su representación numérica:
10 x 10 = 100.
Lo mismo pasa con cualquier moneda:

0,1 x 10 = 1

0,01 x 10 = 0,1
Como podemos observar, si multiplicamos cualquier moneda o billete por 10 el resultado es otra moneda o billete con valor superior. Concretamente 10 veces superior. Por eso en la multiplicación el resultado es igual al multiplicando con la coma desplazada una vez hacia la derecha.
Multiplicación de números decimales con moneda
Una vez sabemos esto podemos pasar a multiplicar un número decimal por 10 y modelizarlo con las monedas.
Vamos a multiplicar 23,14 x 10.
Primero colocamos el dinero en vertical: 23,14
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Luego repetimos 10 veces cada moneda y billete: 23,14 x 10
![]()
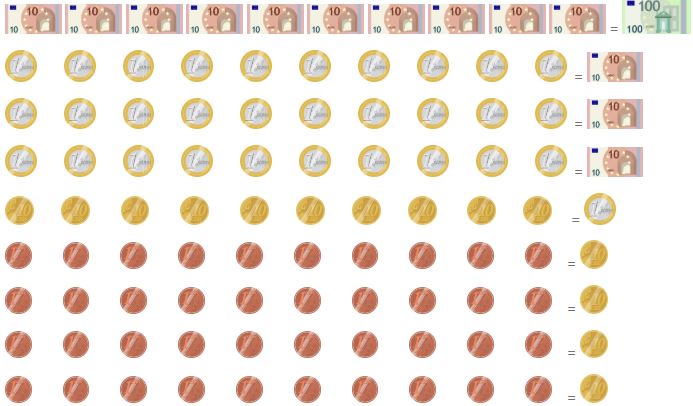
Por último, establecemos las equivalencias con los billetes y monedas correspondientes y las contamos:
![]()
23,14 x 10 = 231,4
Usando como ejemplo el dinero, podemos multiplicar números decimales por 10 y comprender por qué en el resultado la coma se desplaza una vez hacia la derecha. Puedes utilizar billetes y monedas, papeles pintados que los representen o dibujarlas en un papel. Prueba ahora a hacer otras multiplicaciones como 35,12 x 10; 16,43 x10 o las que tú te inventes…
Si quieres conocer más sobre multiplicación de números decimales, materiales manipulativos y otros contenidos de matemáticas de primaria, entra en Smartick y pruébalo gratis.
Para seguir aprendiendo:
- Los números decimales y el uso del dinero
- Números decimales: Multiplicar y dividir por cifras seguidas de ceros
- Suma y resta de números decimales usando dinero como ejemplo
- Divisiones con decimales usando el dinero como ejemplo
- Multiplicar un número decimal por 10
- Características de la práctica significativa - 23/03/2020
- Cómo representar fracciones en la recta numérica - 10/02/2020
- Diagramas de Venn en Smartick - 13/01/2020








Hola, me gustaría saber si tenéis juegos para empezar a aprender, es para mi sobrino tiene un añito y medio y no se si hay algún método para esta edad, he visto un poquito vuestros proyecto y demás y es muy interesante. Gracias, espero vuestra respuesta.
Un saludo
Hola Carolina:
El método Smartick está pensado para niños a partir de 4 años. No es un juego, es un método de aprendizaje de matemáticas 😉
¡En nada de tiempo tu sobrino podrá empezar a aprender mates con nosotros!
Nos alegra que te haya gustado Smartick.
¡Un saludo!
Una vez que finalice el período de prueba cual es su costo
Hola Sonia:
El coste de Smartick depende del número de alumnos que se apunten, la duración de la suscripción y la divisa con que se pague. ¡Tenemos alumnos en más de 100 países!
Te recomiendo que te registres en el periodo gratuito de prueba para conocer el producto en profundidad. Con tu usuario de tutor y contraseña puedes acceder a las tarifas que aplican en tu caso.
Si te surge cualquier duda adicional, puedes contactar en todo momento con nuestros compañeros de atención al cliente en [email protected]
¡Un saludo!