En este post vamos a aprender a calcular medios, tercios, cuartos y quintos. Estas expresiones no solo se utilizan en problemas matemáticos sino también en la vida cotidiana.
¿Sabes qué son? ¿Sabes cómo se calculan? Vas a ver lo fácil que es calcular medios, tercios, cuartos y quintos.
Las expresiones “un medio” o “la mitad”, “tercios” o “la tercera parte”, “un cuarto” o “la cuarta parte”, «un quinto» o «la quinta parte» son las fracciones que más usamos en nuestra vida cotidiana. Las empleamos cuando nos referimos a elementos que están divididos en partes iguales o que pueden dividirse en partes iguales.
Índice
Un medio
Qué es un medio
Un medio equivale a la fracción \(\frac{1}{2}\), por lo tanto un medio es la mitad de una cantidad. Se calcula dividiendo por 2.
También fuera de las matemáticas habrás escuchado muchas veces: “Tengo medio sándwich”.
Cómo calcular un medio
Calcular un medio es dividir entre dos, por eso media hora son 30 minutos, 60 minutos entre dos.
Si lo que tenemos son varios medios, por ejemplo, cuatro medios de 18 = \(\frac{4}{2}\) de 18, lo que hay que hacer es lo siguiente:
- Primero hay que dividir entre 2 el número 18, que queda 9.
- Después se multiplica el numerador de la fracción (4) por el 9 que nos había salido de la anterior división.
- Y nos quedaría hacer la multiplicación 4 × 9 = 36.
Ejemplos de medios
Un medio de 10 = \(\frac{1}{2}\) de 10 = \(\frac{10}{2}\) = 5
Un medio de 34 = \(\frac{1}{2}\) de 34 = \(\frac{34}{2}\) = 17
Tres medios de 14 = \(\frac{3}{2}\) de 14 = 3 × \(\frac{14}{2}\) = 3 × 7 = 21
Un tercio
Qué es un tercio
Un tercio equivale a la fracción \(\frac{1}{3}\), por lo tanto un tercio es la tercera parte de una cantidad.
Hay muchos ejemplos de la vida cotidiana en los que expresamos cosas como: “¡Te has comido un tercio de mi chocolatina!”
Cómo calcular un tercio
Si quieres calcular varios tercios de alguna cantidad, por ejemplo, seis tercios de 24 = \(\frac{6}{3}\) de 24, tienes que hacer lo siguiente:
- Primero, hay que dividir entre 3 el número 24, que queda 8.
- Después, se multiplica el numerador de la fracción (6) por el 8 que nos había salido de la anterior división.
- Y nos quedaría hacer la multiplicación 6 × 8 = 48.
Ejemplos de tercios
Un tercio de 24 = \(\frac{1}{3}\) de 24 = \(\frac{24}{3}\)= 8
Un tercio de 33 = \(\frac{1}{3}\) de 33 = \(\frac{33}{3}\) = 11
Cinco tercios de 15 = \(\frac{5}{3}\) de 15 = 5 × \(\frac{15}{5}\) = 5 × 5 = 25
Un cuarto
Qué es un cuarto
Un cuarto equivale a la fracción \(\frac{1}{4}\). Un cuarto es la cuarta parte de una cantidad y se calcula dividiendo por 4. Seguramente has dicho alguna vez: “Falta un cuarto de hora para que comience la película”, como sabrás, un cuarto de hora es la cuarta parte de 60 minutos, 60 : 4 = 15, 15 minutos.
Cómo calcular un cuarto
Para calcular fracciones de cantidades que tengan denominador cuatro, por ejemplo, nueve cuartos de 36 = \(\frac{9}{4}\) de 36.
- Primero, hay que dividir entre 4 el número 36, que queda 9.
- Después, se multiplica el numerador de la fracción (9) por el 9 que nos había salido de la anterior división.
- Y nos quedaría hacer la multiplicación 9 × 9 = 81.
Ejemplos de cuartos
Un cuarto de 20 = \(\frac{1}{4}\) de 20 = \(\frac{20}{4}\) = 5
Un cuarto de 28 = \(\frac{1}{4}\) de 28 = \(\frac{28}{4}\) = 7
Siete cuartos de 8 = \(\frac{7}{4}\) de 8 = 7 × \(\frac{8}{4}\) = 7 × 2 = 14
Un quinto
Qué es un quinto
Un quinto equivale a la fracción \(\frac{1}{5}\), por lo tanto los quintos son la quinta parte de una cantidad. Se calcula dividiendo por 5.
Antiguamente se llamaba «quintos» a los soldados que iban al servicio militar obligatorio, porque se obligaba a ir al ejercito a una quinta parte de los que cumplían la mayoría de edad.
Cómo calcular un quinto
Calcular un quinto es muy sencillo, solo tienes que dividir entre cinco.
Si tienes que calcular varios quintos, por ejemplo, diez quintos de 55 = \(\frac{10}{5}\) de 55, tienes que hacer lo siguiente:
- Primero, hay que dividir entre 5 el número 55, que queda 11.
- Después, se multiplica el numerador de la fracción (10) por el 11 que nos había salido de la anterior división.
- Y nos quedaría hacer la multiplicación 10 × 11 = 110.
Ejemplos de quintos
Un quinto de 40 = \(\frac{1}{5}\) de 40 = \(\frac{40}{5}\) = 8
Un quinto de 10 = \(\frac{1}{5}\) de 10 = \(\frac{10}{5}\) = 2
Tres quintos de 35 = \(\frac{3}{5}\) de 35 = 3 × \(\frac{35}{5}\) = 3 × 7 = 21
Problema: Medios, tercios y cuartos
Ana, Verónica y Pablo fueron ayer al supermercado. Cada uno compró una docena de huevos porque estaban en oferta. Al llegar a casa, Ana ha hecho una tortilla usando un tercio de su docena de huevos, Pablo ha hecho huevos revueltos con la mitad de su docena y Verónica ha utilizado un cuarto de su docena para hacer un pastel. ¿Cuántos huevos han usado cada uno?
En primer lugar debemos recordar que una docena de huevos son 12 huevos. Ahora, vemos los datos que nos dan:
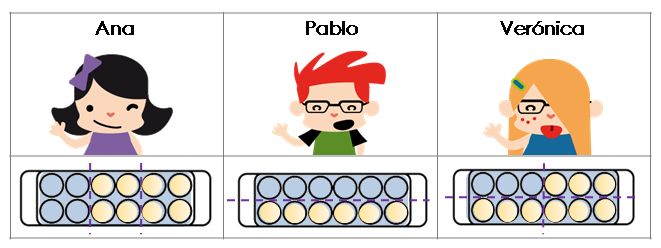
- Ana ha utilizado un tercio de su docena de huevos. Si observamos la imagen, vemos que la docena está dividida en tres partes iguales y ha utilizado una de esas partes, es decir, 4 huevos. Podemos calcularlo dividiendo 12 : 3 = 4.
- Pablo ha utilizado la mitad de su docena de huevos. Si observamos la imagen, vemos que la docena está dividida en dos partes iguales y ha utilizado una de esas partes, es decir, 6 huevos. Podemos calcularlo dividiendo 12 : 2 = 6.
- Verónica ha utilizado un cuarto de su docena de huevos. Si observamos la imagen, vemos que la docena está dividida en cuatro partes iguales y ha utilizado una de esas partes, es decir, 3 huevos. Podemos calcularlo dividiendo 12 : 4 = 3.
Problema: Quintos
Para rellenar una piscina ha venido un camión que ha gastado las 3 quintas partes de su depósito, que contenía 18.000 litros de agua. ¿Cuántos litros de agua se han vertido en la piscina?
- Tenemos que calcular \(\frac{3}{5}\) de 18.000.
- Dividimos 18.000 entre 5, resultan 3.600 litros (esa es la quinta parte del depósito, pero se han gastado 3).
- Multiplicamos 3.600 por 3, resultan 10.800 litros, ¡a nadar!
¿Qué te ha parecido? Si este post te ha sido útil, ¡compártelo con tus amigos!
Y si quieres aprender más matemáticas de primaria, regístrate gratis en Smartick y ¡disfruta de las matemáticas!
Para seguir aprendiendo:
- Explicación de un medio, dos tercios o un cuarto con algunos problemas
- Introducción a las fracciones
- Barras de Singapur aplicadas a las fracciones
- Ejercicios de números proporcionales
- Tablas de dividir
Sara es parte del equipo de desarrollo de contenidos y didáctica de Smartick Matemáticas, responsable de las áreas de álgebra y lógica.
Es muy buena está aplicación aprendí a sumar fracciones y a hacerlas.
me ayuda mucho aprender ❤💕💖💗💓💝💞💜
Excelente, volví a estudiar después de 60 años, recién descubro está página es buenísima.
Muy didáctica la explicación, lo que nunca había entendido, en un minuto quedó clarísimo. Gracias por compartir.
Me ayudó bastante.
Es muy bueno
Muy bueno tus aportes publicados, gracias.
Muy bien. Disfruto mucho, ¡muchas gracias!
Muchas gracias muy buen tema
Es fantástico
Muy bueno
Excelente explicación, es una herramienta valiosa.
Muchas gracias por tu ayuda. Saludos
Grandioso método… Me gusta me gusta, se aprende muy bien!!!
¡Que bien Hugo!, muchas gracias por tu comentario 👍