En el post de hoy vamos a comentar unas actividades incorporadas recientemente en las sesiones de Smartick Matemáticas. Es un tema del que hay abundante literatura científica y, como el método Smartick está basado en evidencias, no queríamos que nuestros alumnos se perdieran las series de crecimiento.
Índice
Qué es una serie de crecimiento
Las series de crecimiento, también conocidas como patrones de crecimiento o growing patterns, son series, como su nombre indica, en las que se da una cierta repetición pero en las varía el número de elementos de cada figura, aumentando o disminuyendo. Hay que distinguirlas, por tanto, de las series de repetición, en las que se alternan elementos siguiendo una regla más o menos compleja.
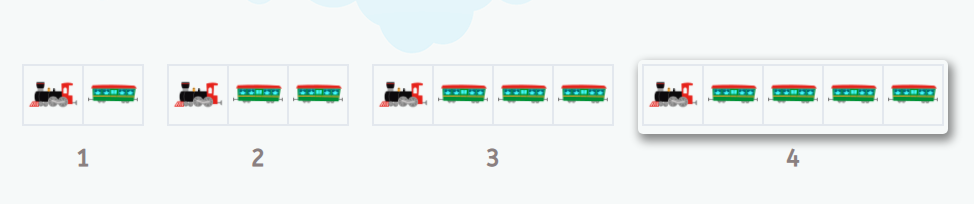
Existe bastante evidencia científica sobre utilizar series de crecimiento desde edades tempranas. Así, los alumnos de Smartick empiezan a trabajar con las series de crecimiento desde los 5 años. En el apartado de bibliografía dejamos varios trabajos científicos sobre series de crecimiento en la escuela. Las series de crecimiento son una muy buena manera de empezar a relacionarse con contenidos de matemáticas avanzadas, como la proporcionalidad, las funciones o los inicios del álgebra. En Smartick vemos las series de crecimiento como una manera más de acercar a nuestros alumnos a resolver problemas, una forma más de hacer matemáticas.
Ejemplos de series de crecimiento
Te presentamos dos ejemplos, uno con objetos cotidianos -mesas y sillas- y otro, más abstracto, con baldosas:
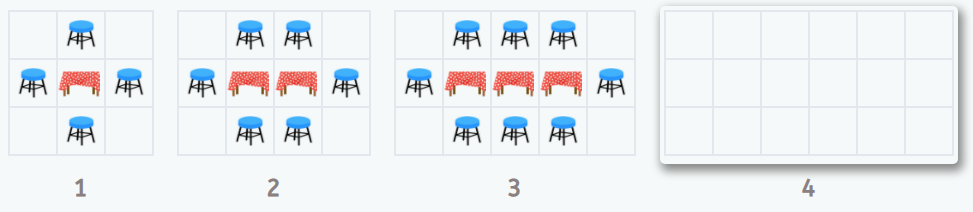
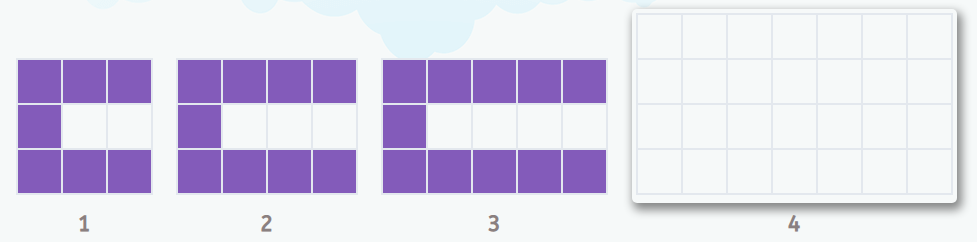
El primer elemento es una especie de C formada de 7 baldosas, los lados de la C se van alargando, añadiendo dos baldosas cada vez, una arriba y otra abajo.
Cómo encontrar la regla de una serie de crecimiento
Una primera pregunta que puede surgir es cuál será el siguiente elemento de la serie.
Se pueden preguntar otras cosas pero siempre están basadas en que sepamos construir el siguiente elemento. La manera de acercarnos a ello es la pista con la que podrás ayudar a tu hijo si tiene que resolver una serie de crecimiento: buscar la figura anterior en la siguiente.
Fíjate en el siguiente ejemplo, sacado de una de las actividades iniciales de la trayectoria de aprendizaje de series en Smartick Matemáticas. En este caso se da construida parte de la figura 4, ¿qué parte? Justamente la que corresponde con la figura 3.
Cómo se enseñan las series de crecimiento
Como decíamos en el epígrafe anterior, todo comienza aprendiendo a construir el siguiente elemento. En un primer momento se le presentan tres elementos construidos -no interactivos- junto a un tablero en el que ya está construida parte del cuarto elemento, la parte que se corresponde al elemento tercero. Este tablero tiene las filas y columnas justas, que es otra forma de ayudar -un andamio, decimos en didáctica- al alumno a empezar a resolver estos problemas.
Posteriormente se irá retirando parte de ese andamio, conforme el niño va aprendiendo y superando las primeras dificultades. Observa el siguiente ejemplo:
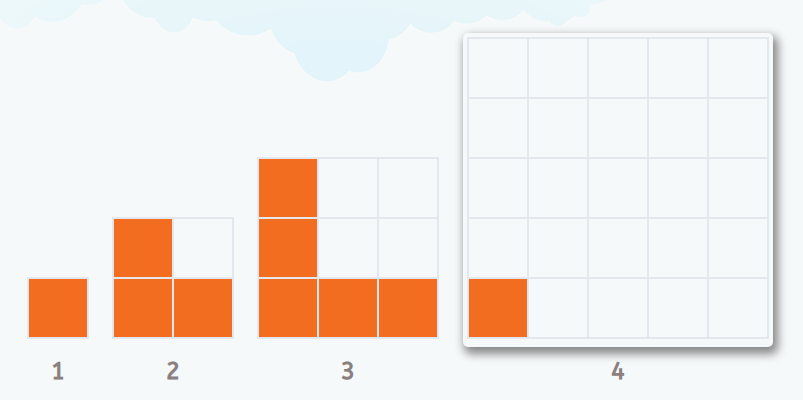
La primera figura tiene una baldosa, la segunda, tres, la tercera 5. Parece que van a ser los números impares y que la forma que va a tener que completarse en la figura 4 es como una L. Así es, los números impares se presentan también con este curioso patrón. También son los números impares los del ejemplo anterior, el de los patines, ¡con otro patrón distinto!
Una vez que el niño ha aprendido a construir la siguiente figura se le va a pedir que diga cuántos elementos la componen. Esto es lo último que harán con series de crecimiento en primeras edades, pero volverán más adelante, a mediados de primaria.
Los alumnos más mayores tendrán que decir cuántos elementos va a tener una «figura cercana», la figura 5, para ello solo dispondrán de lo que han aprendido de series de crecimiento y de las cuatro figuras que les damos construidas. Tendrán que ser capaces para ello de identificar el patrón, como decíamos antes, reconocer la figura anterior en la siguiente y ver qué se está añadiendo de nuevo cada vez.
Los niños más mayores, entre primaria y secundaria, trabajan con los elementos lejanos de las series de crecimiento, ¿cuántos elementos tendría la figura 10? ¿Y la figura 20? Esto, que puede parece difícil en un primer momento, es clave para construir el patrón numérico de la serie, ya que en el caso de las figuras cercanas podíamos limitarnos casi a contar. Los patrones que siguen las series de crecimiento suelen ser lineales, esto es, a cada paso se va añadiendo el mismo número de elementos, aunque llegados a este punto se suman también algunos patrones cuadráticos, como los de este ejemplo:
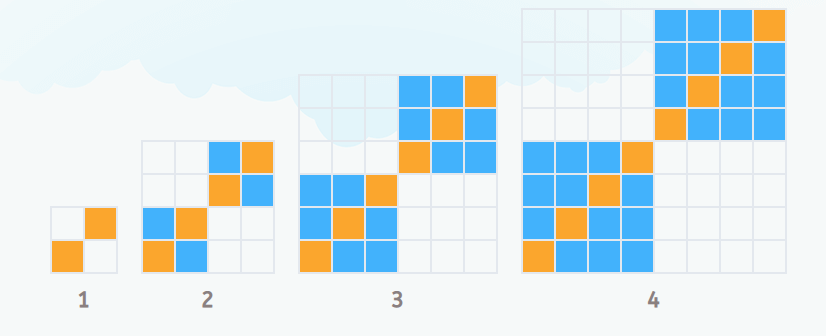
La figura 1 tiene dos baldosas (dos cuadrados) la figura 2 tiene 8 baldosas (dos cuadrados de lado dos), la tercera 18 (dos cuadrados de lado 3), etcétera. ¿Cuántas baldosas tendrá la figura 10? 200, ya que serán dos cuadrados de lado 10, con 100 baldosas cada uno. A estas alturas del currículo, los alumnos deberán ser capaces también de identificar con letras la expresión que tendría en función de n, la figura que ocupa ese preciso lugar, el enésimo.
Qué hay en Smartick antes de las series de crecimiento
Antes de poder enfrentarse a problemas de series de crecimiento los alumnos deben haber mostrado cierta fluidez resolviendo patrones matemáticos y series de repetición.
Con qué contenidos de matemáticas están conectadas las series de crecimiento
Como hemos visto a lo largo de este artículo, las series de crecimiento están relacionadas con el conteo, pero también con el pensamiento funcional y el álgebra, a través de las sucesiones y las progresiones aritméticas, la proporcionalidad y las funciones. No es poca cosa.
Si quieres saber más sobre patrones matemáticos, puedes consultar este post de nuestro blog sobre series, qué son y para qué sirven.
Pero si prefieres practicar ejercicios de series y patrones y más matemáticas de primaria adaptadas a tu nivel, entra en Smartick, regístrate y pruébalo gratis.
Bibliografía sobre series de crecimiento
Para seguir aprendiendo:
- Qué son los patrones matemáticos: tipos y ejemplos
- Series, qué son y para qué sirven
- ¿Cuál es la diferencia entre serie y patrón?
- Series unidimensionales
- algebra tiles«>Cómo restar polinomios con la ayuda de algebra tiles
Es formador de maestros, tanto en formación inicial en la Facultad de Educación de la Universidad Complutense de Madrid como en formación continuada. Apasionado de tocar las matemáticas.
Forma parte del equipo de Didáctica de Smartick.
Autor del blog Tocamates y del libro “Y me llevo una”.
Le encanta la divulgación y -en general- la comunicación. No calla ni debajo del agua, de ahí que colabore con varias radios y medios de comunicación, y que si tiene un rato, se eche unos largos en la piscina.
- El lenguaje de funciones y gráficas - 14/02/2024
- Cómo aplicar la jerarquía de operaciones - 20/09/2023
- Expresiones algebraicas: ¿Qué son? ¿Para qué sirven? - 21/07/2023