Las fórmulas matemáticas nos permiten expresar y resolver problemas en diversas disciplinas. En este post vamos a ver qué son, cómo se componen y los tipos de fórmulas que existen. Por último, conoceremos algunas de las fórmulas más usadas.
Índice
¿Qué es una fórmula matemática?
Una fórmula es la manera que utilizamos para resolver o ejecutar una situación o problema difícil. En matemáticas, una fórmula es la expresión que relaciona diferentes cantidades o variables mediante operaciones matemáticas como la suma, la resta, la multiplicación y la división.
Las fórmulas matemáticas no solo se utilizan en matemáticas puras, sino que también se aplican en una amplia variedad de áreas, incluyendo física, química, ingeniería, economía, estadísticas, informática, entre otros. Por ejemplo, en física, las leyes del movimiento de Newton se expresan mediante fórmulas matemáticas como F = m x a (fuerza igual a masa por aceleración), mientras que en economía, la ley de la oferta y la demanda se puede expresar mediante una fórmula que relaciona el precio de un bien con la cantidad demandada y ofrecida.
Elementos que componen a las fórmulas matemáticas
Hay tres elementos fundamentales que componen una fórmula:
- Las variables, hacen referencia a las incógnitas, es decir, la cantidad de la que no tenemos su valor.
- Las constantes, son los valores numéricos que se mantienen igual.
- Los operadores, son los símbolos que utilizamos en matemáticas para resolver cualquier operación; por ejemplo: suma (+), resta (-), multiplicación (x), división (÷) y el de igualdad (=).
Por ejemplo, en la fórmula L= 2 · π · r, donde L (longitud de la circunferencia) es lo que se quiere calcular, el número 2 y el número Π son las constantes, la operación es la multiplicación y r, el radio de la circunferencia, es la variable.

Algo muy interesante de las fórmulas matemáticas es que se comportan como una relación, esto es, en la expresión anterior podríamos calcular r (radio de la circunferencia), si disponemos del valor de L. Para ello, despejaríamos r siguiendo las reglas de las ecuaciones y quedaría r = L / (2π).
En las fórmulas matemáticas también podemos encontrar otro tipo de elementos como: vacío (ø), integral (ʃ), sumatoria (Ʃ), entre otros.
Tipos de fórmulas
Como hemos mencionado antes, las fórmulas matemáticas se pueden utilizar para distintas ocasiones, depende de la complejidad y función, podemos clasificarlas en:
- Fórmulas algebraicas: son aquellas expresiones matemáticas que combinan letras y números, y que van unidas con los signos de las operaciones matemáticas. Las expresiones algebraicas nos sirven para describir situaciones y relaciones matemáticas en términos generales. Esto es, en situaciones en las que no todos los valores son conocidos. Nos permiten expresar fórmulas, ecuaciones y modelos matemáticos de manera abstracta, lo que facilita el análisis y la resolución de problemas.
Ejemplo: ax² + bx² + c = 0
- Fórmulas geométricas: son aquellas que expresan relaciones entre las medidas de las figuras geométricas. Por ejemplo: el área de un círculo o el volumen de un prisma.
A= π · r²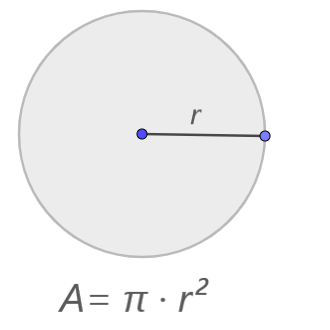
Imagen realizada con GeoGebra - Fórmulas trigonométricas: en este tipo de fórmulas encontramos una relación matemática entre las funciones trigonométricas como seno, coseno, tangente, cotangente, secante y cosecante. Este tipo de fórmulas se utilizan para resolver una variedad de problemas en matemáticas, física, ingeniería y otras disciplinas.
- Fórmulas de cálculo diferencial e integral: son utilizadas para calcular derivadas e integrales.
Estas son solo algunos ejemplos de las tantas fórmulas que hay. Hay muchas otras técnicas y fórmulas específicas para resolver problemas más avanzados y situaciones particulares.
Las fórmulas matemáticas son herramientas poderosas que nos permiten comprender, modelar y resolver una amplia variedad de problemas en diferentes disciplinas. Ya sea que estemos calculando la trayectoria de un proyectil, optimizando una cadena de suministro o diseñando un algoritmo, las fórmulas matemáticas son nuestra guía en el vasto universo del conocimiento. Existen importantes ecuaciones que han aportado grandes cambios en la historia.
Esperamos que la entrada haya sido de tu agrado, no dudes en compartirla o en proponer temas de los que te gustaría saber. Para aprender más, regístrate en Smartick, el método online de aprendizaje de matemáticas y comprensión lectora para niños de 4 a 14 años.
Para seguir aprendiendo:
- La división en matemáticas: una operación imprescindible
- Figuras geométricas: El círculo
- Introducción a las ecuaciones: Cómo resolverlas fácilmente con ejemplos
- ¿Cómo se resuelven los problemas de ecuaciones?
- Expresiones algebraicas. ¿Qué son? ¿Para qué sirven?







