¿Te parece difícil manejar un diagrama de Venn? ¿No tienes clara cuál es su utilidad? En esta entrada intentaremos aclarar tus dudas, explicándote brevemente cómo dominar esta técnica.
Índice
Silogismos y proposiciones categóricas
Empecemos señalando que utilizaremos el diagrama de Venn para evaluar argumentos o silogismos, es decir, para determinar si es un argumento válido o no. Pero no argumentos de cualquier tipo. En concreto, argumentos deductivos.
Recordemos que la característica más importante de estos argumentos es que:
1) La conclusión se sigue necesariamente de las premisas, lo cual no sucede en los argumentos inductivos, que son ampliativos (es decir, argumentos en los que la conclusión contiene más información que las premisas). Por eso decimos que entre premisas y conclusión existe una relación de consecuencia lógica. Por ejemplo, este un argumento deductivo:
Todos los caballos son blancos.
Todas mis mascotas son caballos.
Luego, todas mis mascotas son blancas.
Destaquemos también que:
2) Estas premisas son siempre proposiciones categóricas, y que estas proposiciones categóricas 3) ponen en relación tres términos, que tradicionalmente se denominan “término mayor”, “término menor” y “término medio”. Veamos en detalle estos dos puntos.
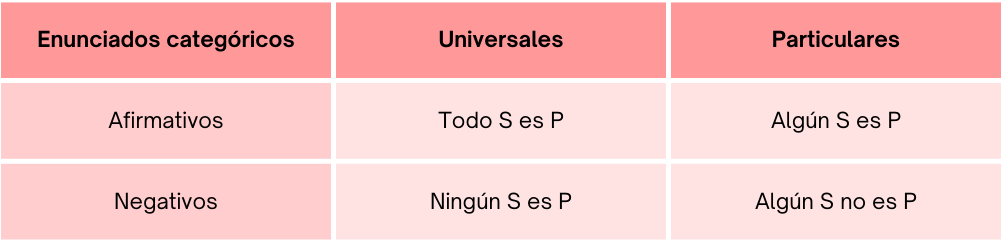
¿Qué es una proposición categórica? Llamamos así a oraciones que adoptan las siguientes tipologías:
- Todo A es B. Por ejemplo: “Todos los caballos son cuadrúpedos”.
- Ningún A es B. Por ejemplo: “Ningún pato es una ardilla”.
- Algún A es B. Por ejemplo: “Algunos cisnes son blancos”.
- Algún A no es B. Por ejemplo: “Algunos números no son impares”.
Las dos primeras se denominan “categóricas universales”, mientras que las otras dos se denominan “categóricas particulares”, y según los cuantificadores, en ambos casos disponemos de una afirmativa y otra negativa. Tradicionalmente, se las reconoce mediante una vocal: las categóricas universales afirmativas, es decir, aquellas cuyo cuantificador es «todo», con la A; las universales negativas que se introducen con «ningún», con la E. La I representa, en cambio, las categóricas particulares afirmativas, y la O, por último, las particulares negativas. Son los cuatro tipos de proposiciones que encontraremos en los diagramas de Venn.
En cuanto a los términos que contienen, veamos de qué se trata con un ejemplo:
- [premisa] Todos los koalas son simpáticos.
- [premisa] Algunos animales son koalas.
- [conclusión] Algunos animales son simpáticos.
En este argumento hay en juego tres términos: koalas, simpáticos y animales. Animales es el sujeto de la conclusión, y aparece también en la segunda premisa. A este se le denomina “término menor”, y, por extensión, la premisa en la que aparece se denomina “premisa menor”. En cambio, “simpáticos”, que es el predicado de la conclusión, recibe el nombre de “término mayor”, y su premisa, “premisa mayor”. El término que aparece en las premisas, pero no en la conclusión, es el “termino medio”, es decir, aquel que está en medio del mayor y del menor, relacionándolos.
En este vídeo se puede consultar más información sobre este tema:
Figuras y modos silogísticos
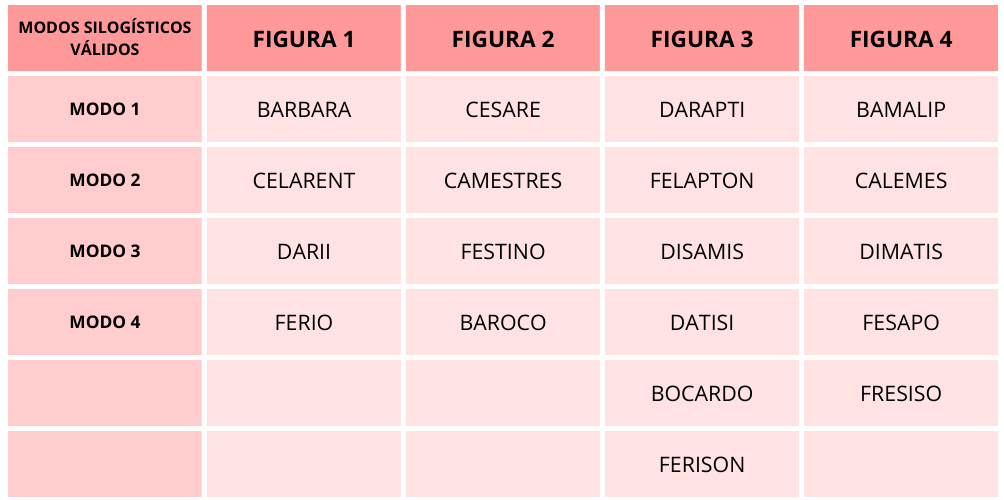
Estos tres términos dan para muchas combinaciones. Así lo ha puesto de manifiesto la tradición aristotélica y medieval, que ha identificado cuatro formas lógicas o “figuras”, en las que aparecen los tres términos en diferentes posiciones.
A partir de estas cuatro figuras, se han repertoriado un total de 256 modos o argumentos; 64 por figura. Estos modos son el resultado de combinar figuras silogísticas y proposiciones categóricas. Imaginemos, por ejemplo, que tomamos las proposiciones categóricas universales afirmativas, y utilizamos como molde la primera figura. Así obtendríamos este argumento:
- [premisa] Todos los caballos [H] son cuadrúpedos [G].
- [premisa] Todas mis mascotas [F] son caballos [H].
- [conclusión] Todas mis mascotas [F] son cuadrúpedos [G].
Dado que son todas proposiciones tipo A, representaremos este argumento como A-A-A. Ya tendríamos un modo. Ahora probemos con esto:
- [premisa] Ningún ser humano [H] es alpinista [G].
- [premisa] Todos los europeos [F] son seres humanos [H].
- [conclusión] Ningún europeo [F] es alpinista [G].
La primera premisa es una proposición tipo E, como la conclusión, mientras que la segunda premisa es una tipo A. Tenemos, por tanto, un modo E-A-E basado también en la primera figura lógica. Como es manifiesto, la misma posición de los términos mayor, menor y medio, a los que nos referimos con las letras G, F y H, proporciona diferentes tipos de argumentos de acuerdo con las proposiciones que utilicemos.
Ahora bien, de acuerdo con lo dicho anteriormente, para que un argumento deductivo sea correcto, la conclusión debe seguirse necesariamente de las premisas. Si un argumento cumple este requisito, decimos que se trata de un argumento válido. Pues bien, de todos los modos o argumentos que pueden formar, un total de 256, solo identificamos como válidos una pequeña parte. Depende del enfoque que se adopte, 19 o 24. Sea como sea, lo que nos interesa aquí es saber que cada silogismo tiene un nombre, asignado por la tradición lógica para su memorización, en cuyas vocales se esconde el tipo de proposición categórica utilizada.
Ahora bien, ¿en qué se diferencia un modo válido de otro no válido? Veamos un ejemplo. Tomemos la primera figura, y utilicemos nada más que proposiciones categóricas universales. Las que simbolizamos con la A. Un posible argumento (A-A-A) sería este:
Ahora utilicemos los mismos términos: caballos, cuadrúpedos y mascotas, respetando el orden del anterior argumento, pero, en lugar de categóricas universales negativas, tipo E (le llamaremos E-E-E).
- [premisa] Ningún caballo es bípedo.
- [premisa] Ninguna de mis mascotas es un caballo.
- [conclusión] Ninguna de mis mascotas es bípeda.
Si se presta atención a la conclusión de ambos argumentos, se observará que en A-A-A, la conclusión se sigue necesariamente de las premisas, pero no es el caso en el E-E-E. Puede ser que ningún caballo sea bípedo, y también que alguien no tenga, entre sus mascotas, un caballo. Pero, ¿quiere eso decir que ninguna de sus mascotas sea bípeda? No. Alguien puede no tener un caballo como mascota, y sí, en cambio, una mascota que sea bípeda. Un diagrama de Venn sirve para descubrir si un argumento es válido o no en este sentido. Se trata de una técnica sencilla, como explicamos a continuación.
La técnica de un diagrama de Venn
Para utilizar un diagrama de Venn, seguiremos dos estrategias: vaciar espacios u ocupar espacios. De hecho, es un ejercicio que ya contamos en posts anteriores. Solo hay que recordar esto:
- cuando queramos representar proposiciones universales (las tipo A y E), marcaremos los espacios como vacíos,
- y como no vacíos cuando se trate de proposiciones particulares (las tipo I y O).
Si decimos «vaciar» es porque representar una proposición como Ningún perro es bípedo, exige marcar como vacíos aquellos espacios del diagrama donde coinciden perros y bípedos; si la proposición, en cambio, es del tipo Todos los perros son cuadrúpedos, se marcan como vacíos aquellos espacios que contengan perros no cuadrúpedos.
En el caso de Algún perro es cuadrúpedo, representaremos como no vacío el espacio de intersección de perros y cuadrúpedos, mientras que si Algún perro no es cuadrúpedo, la clave es reconocer como no vacío el espacio donde no coinciden ambos elementos.
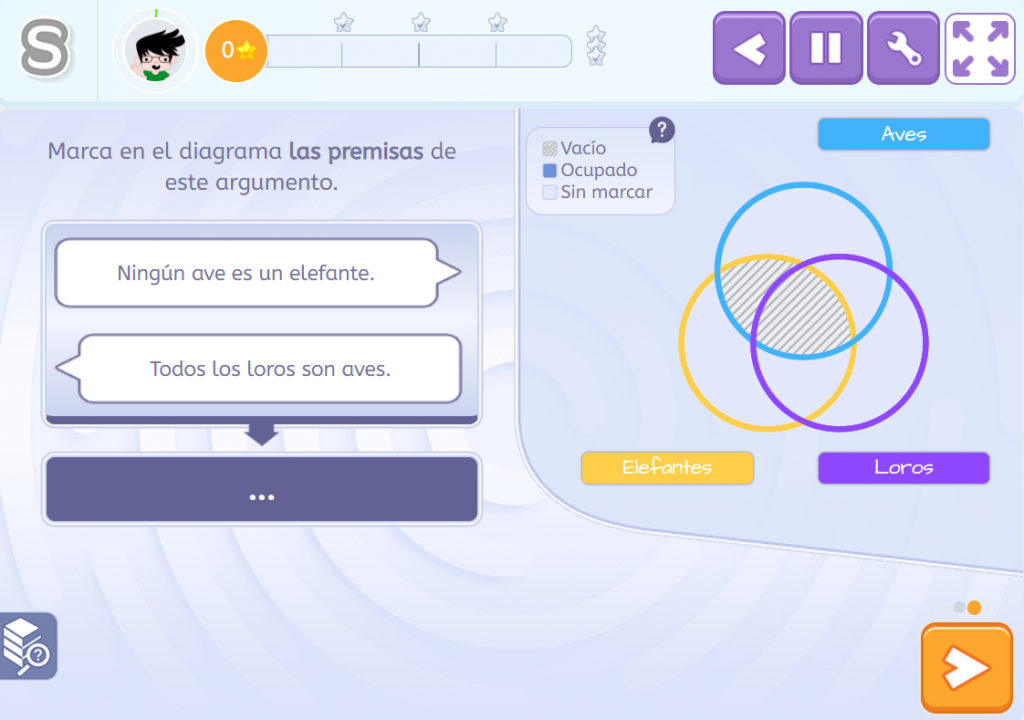
Veamos algunos ejemplos. Aquí se trata de marcar la primera premisa: Ningún ave es un elefante. Primero, identificamos la zona de intersección donde coinciden aves y elefantes, pues estamos tratando de elementos que, supuestamente, comparten el ser ave y el ser elefante. Ahora, como lo que nos indica la proposición es que no hay elementos que posean ambas propiedades, marcamos el espacio como vacío; como si dijéramos no hay aves que sean, al mismo tiempo, elefantes o elefantes que sean, al mismo tiempo, aves.
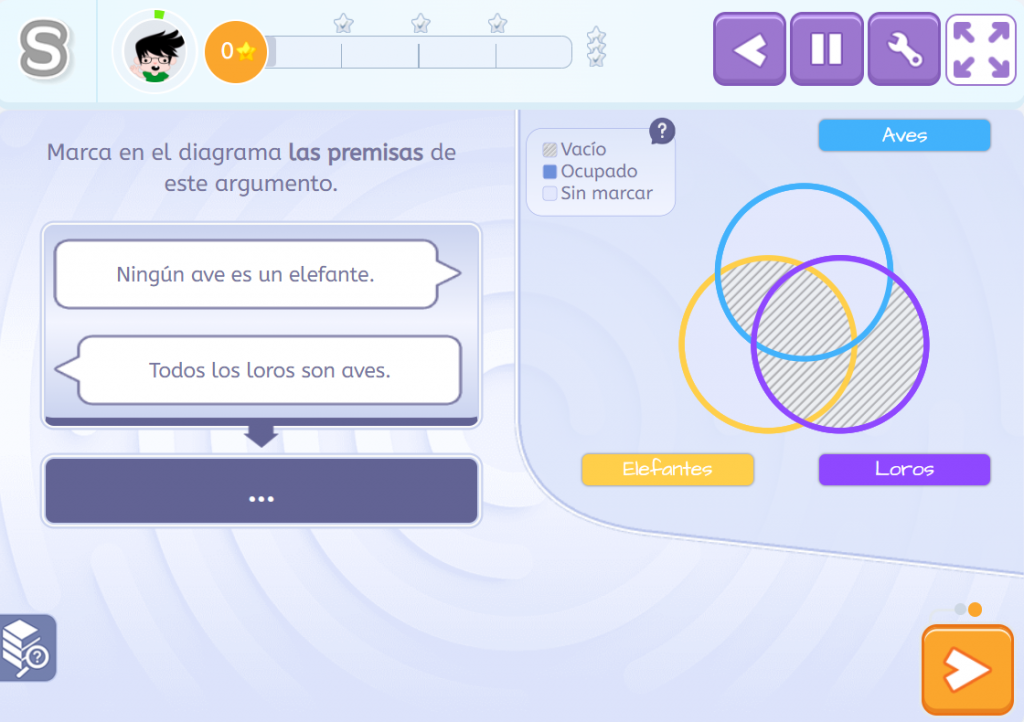
Veamos ahora cómo representar la segunda premisa: Todos los loros son aves. De acuerdo con el diagrama, si hablamos de loros y aves (nos olvidamos ahora de los elefantes), podemos decir que disponemos de dos espacios, uno en el que diríamos que solo hay loros (loros que no son también aves), y otro, el de intersección entre loros y aves, que nos indica que todos los elementos que contiene poseen ambas propiedades: ser loro y ser ave.
¿Qué hacer ahora? Pues, como los elementos a los que se refiere la proposición son loros y aves al mismo tiempo, es decir, son elementos que poseen ambas propiedades, nos vamos a fijar en el espacio donde solo hay loros. Y ese lo marcamos como vacío: dado que todos los loros son aves, no hay loros que sean solo loros. Así que los espacios donde los loros son solo loros, deben estar vacíos.
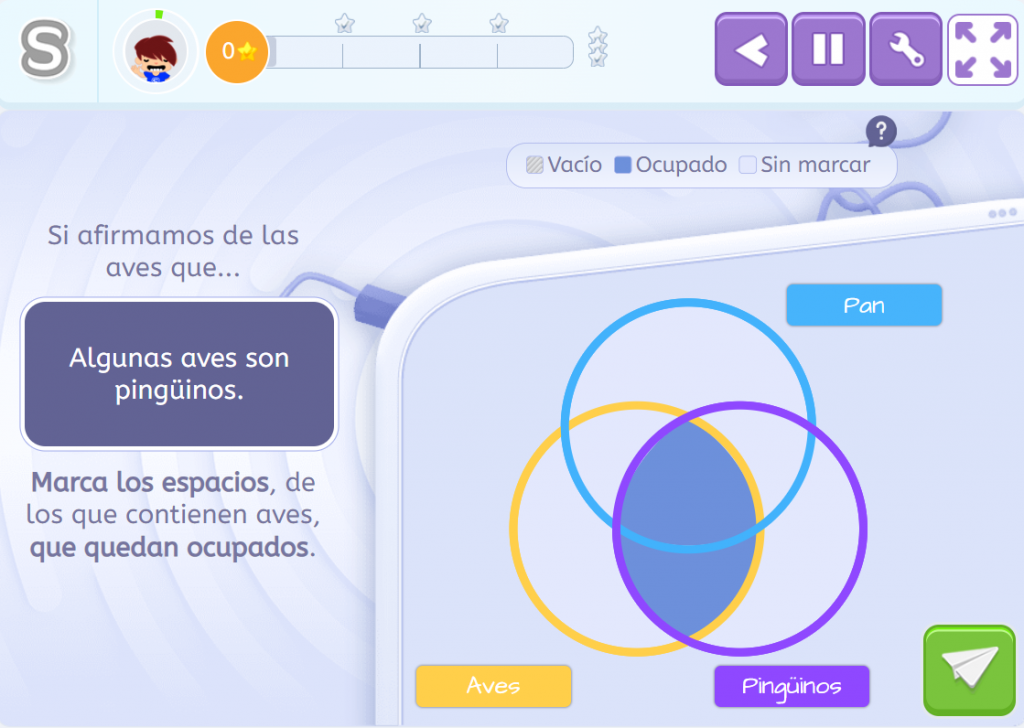
Conforme a lo dicho, en el caso de las proposiciones introducidas por «algún» o «algunos», los espacios ya no se marcan como vacíos, sino como ocupados. En el caso siguiente, representamos la proposición Algunas aves son pingüinos. Como hemos hecho antes, nos fijamos en los espacios donde, hipotéticamente, se encuentran los elementos que poseen ambas propiedades: ser aves y ser pingüinos.
Y como sabemos que hay algún elemento que satisface ambas condiciones, es decir, que es ave y pingüino al mismo tiempo, podemos concluir que el espacio correspondiente no puede estar vacío. Por tanto, lo marcamos como «ocupado».
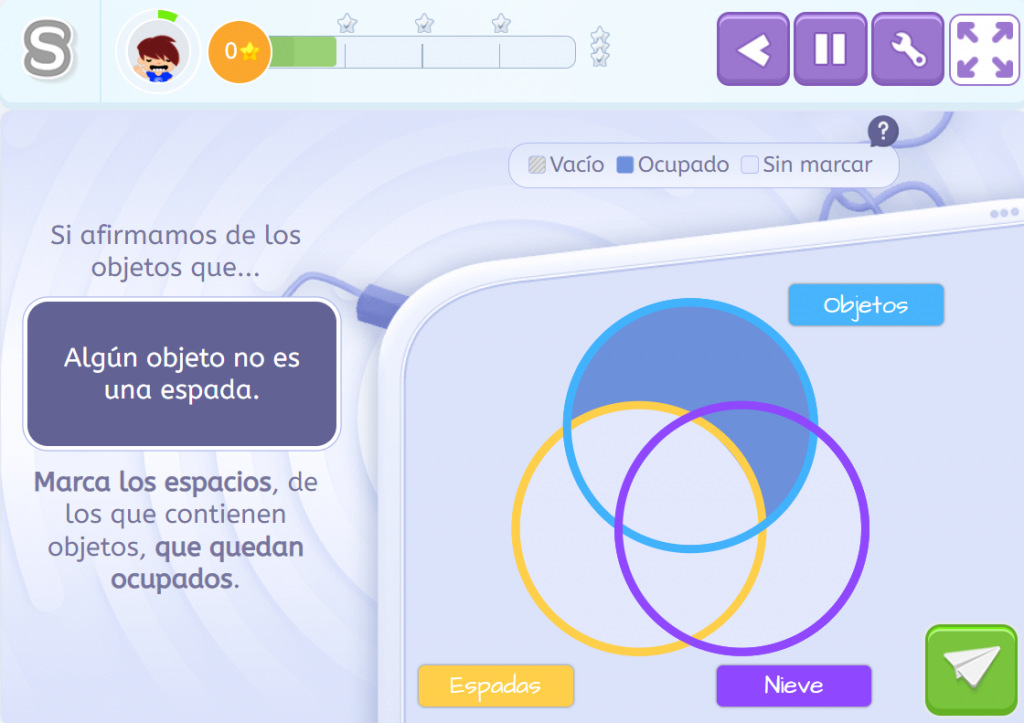
Si debemos representar una proposición tipo O, como la siguiente, el mecanismo es el mismo. Pero, en lugar de fijarnos en el espacio donde los elementos comparten propiedades, prestaremos atención al espacio donde los elementos tan solo satisfacen una condición. Por ejemplo, aquí sabemos que Algún objeto no es una espada. Por tanto, no nos interesan los elementos que son objetos y espadas al mismo tiempo. Nos interesan los objetos que no son espadas, y en tanto que tal, marcamos como no vacío su espacio de representación.
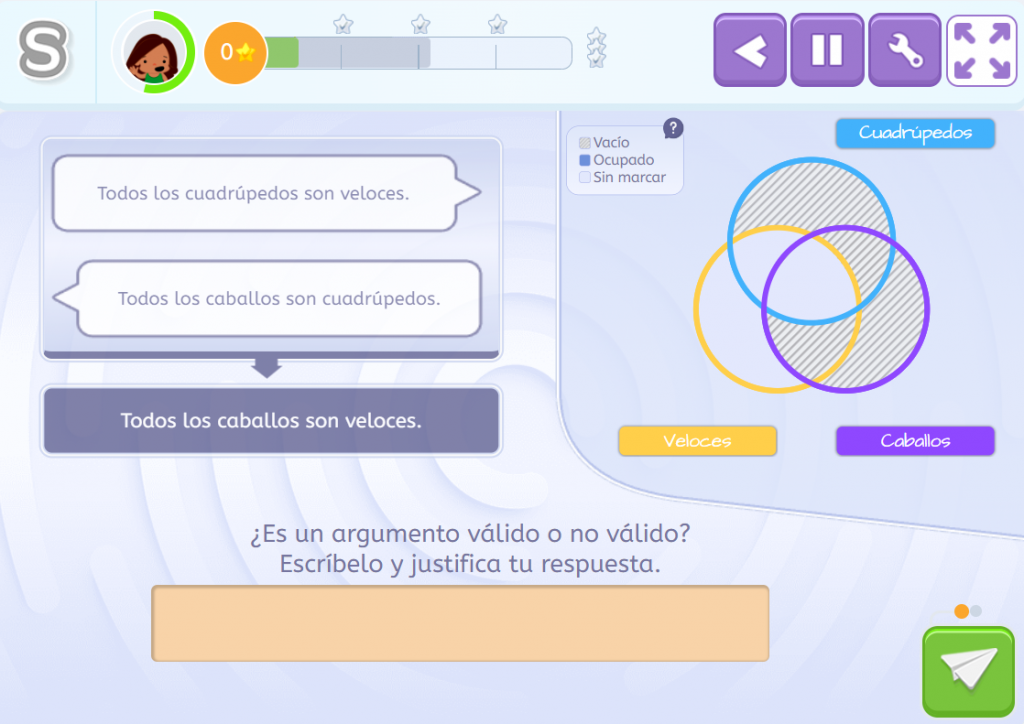
Retomemos ahora uno de los ejercicios anteriores y hagámoslo completo. Las dos premisas, Ningún ave es un elefante y Todos los loros son aves, ya están representadas. Como hemos explicado, se trata de marcar como vacíos los espacios en los que los elementos poseen las propiedades de ser ave y elefante (porque no hay tal cosa) y los espacios en donde los loros no son aves o son solo loros (porque todos los loros que hay, son también aves).
¿Qué responderíamos a la pregunta sobre si es un argumento válido o no? Si recordamos cómo se representan las proposiciones tipo I y O, comprobaremos que en este caso, la conclusión no está representada en el diagrama. Por tanto, afirmaremos que es un argumento no válido. Ahora bien, ¿qué sucede aquí? Todos los caballos son veloces sí está representada. Por tanto, el argumento es válido.
Si quieres que tus hijos comiencen Smartick Thinking y mejoren sus habilidades de pensamiento, no dejes pasar más tiempo; y si tienes dudas, contacta con Smartick. Además, te invitamos a que os registréis en Smartick y lo probéis gratis.
Para seguir aprendiendo:
- Conjuntos y diagramas de Venn
- Conjuntos y subconjuntos
- ¿Qué es la lógica y por qué mi hijo debe trabajarla?
- Sudokus: qué son y cómo resolverlos
- La teoría de conjuntos como técnica de estudio
Convencido de los beneficios de enseñar filosofía desde la Educación Primaria.
Formo parte del equipo de Smartick, diseñando contenidos para que los niños aprendan pensamiento crítico con Smartick Thinking.
Me gusta correr y hacer pan.
- Descubre cómo enseñar a tomar decisiones - 23/10/2024
- Diagramas de Venn: Descubre cómo utilizarlos para evaluar argumentos - 24/07/2024
- ¿Cómo se enseña pensamiento crítico? - 27/10/2023