Propiedad asociativa en las multiplicaciones

La propiedad asociativa indica que la forma en que se agrupan los factores no incide en el resultado de la operación: (A x B) x C = A x (B x C)

Sabemos que el volumen de un prisma se calcula multiplicando el área de la base por la altura:

(B x C) x A u³ (unidades al cubo).

Veamos la propiedad asociativa de la multiplicación con un ejemplo más concreto.

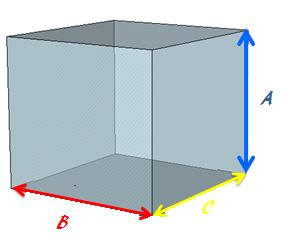
Tenemos un prisma rectangular lleno de agua. Si calculamos la cantidad de agua que necesitamos para llenar este prisma, es decir, el volumen del prisma tenemos:

Base=5 x 2

Altura=10

Volumen = (5 x 2) x 10 = 10 x 10 = 100

El volumen de este prisma rectangular es de 100 u³.

Calculamos el volumen del mismo prisma apoyado sobre otro lado diferente:

Base = 10 x 5

Altura = 2

Volumen = (10 x 5) x 2 = 50 x 2 = 100

De nuevo el volumen es de 100 u³.

Volvemos a calcular el volumen de este prisma apoyado sobre el lado estrecho:

Base = 10 x 2

Altura = 5

Volumen = (10 x 2) x 5 = 20 x 5 = 100

Volvemos a tener un volumen de 100 u³.

Hemos calculado el volumen del mismo prisma de tres maneras diferentes y como debía ser nos da el mismo volumen en las tres ocasiones.

Así, observamos que la manera de agrupar los números a la hora de multiplicar no cambia el resultado.

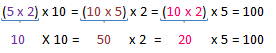
Qué fácil es la propiedad asociativa de la multiplicación, ¿verdad?

Si te ha quedado alguna duda o simplemente quieres ver más ejemplos, visita nuestro tutorial sobre la propiedad asociativa de la multiplicación.

 

Y si quieres aprender más matemáticas de primaria, suscríbete al método Smartick y pruébalo gratis.

Convierte a tus hijos en expertos de las matemáticas

con solo 15 minutos al día

Prueba GRATIS 7 días