En el post de hoy vamos a ver la propiedad distributiva desde el punto de vista geométrico.
Antes de comenzar, podéis consultar estas entradas sobre las propiedades de la multiplicación:
- Repasamos las propiedades de la multiplicación.
- Propiedades de la multiplicación: Distributiva, conmutativa, asociativa, sacar factor común y elemento neutro.
Nosotros vamos a empezar dibujando el siguiente rectángulo rayado, dividido a su vez en otros dos rectángulos más pequeños, uno azul y otro amarillo.
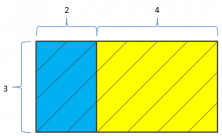
Vamos a calcular primero el área del rectángulo grande rayado que tiene como base (2+4) unidades y altura 3 unidades.
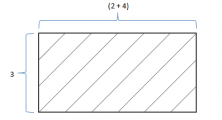
Área = 3 x (2 + 4) unidades
A continuación calculamos las áreas de los dos rectángulos pequeños por separado:
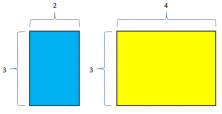
Área del rectángulo azul = (3 x 2) unidades²
Área del rectángulo amarillo = (3 x 4) unidades²
La suma de las áreas de estos dos rectángulos pequeños tiene que dar exactamente la misma que el área del rectángulo grande, ¿verdad? Comprobemos:
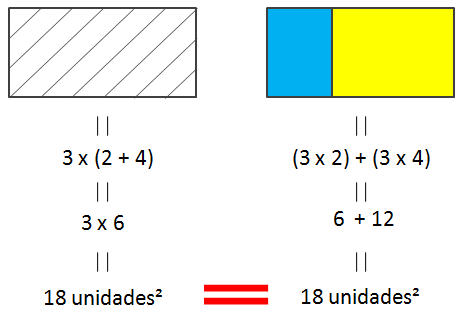
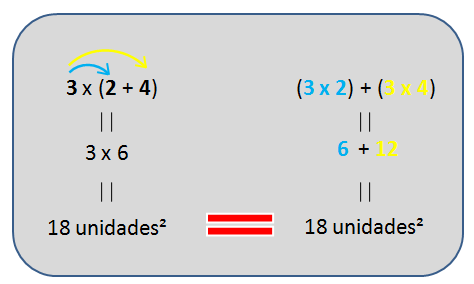
Acabamos de ver que las dos áreas coinciden. Y sin darnos cuenta hemos aplicado lo que llamamos la propiedad distributiva de la multiplicación.
Veamos un ejemplo.
Ejemplo 1.

Y muchos pensaréis, y ¿las operaciones combinadas? Eso del orden a la hora de operar…
Si tenemos 4 · (2+3), lo primero que nos han enseñado a hacer es calcular lo que está dentro del paréntesis 2+3=5 y después hacer la multiplicación 4 · 5 llegando a la solución de 20.
Entonces, ¿cuándo haremos uso de la propiedad distributiva?
Esta propiedad tiene gran parte de su utilidad en el campo del álgebra. Supongamos que queremos resolver la siguiente ecuación:
Ejemplo 2.
5· (x+3) = 25
Aquí no podremos calcular primero el paréntesis ya que x +3 no se puede sumar.
Sin embargo, sí podemos aplicar la propiedad distributiva y nos quedaría:

Ya solo nos quedaría resolver la ecuación.
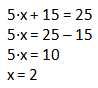
¡Ahora os toca a vosotros practicar!
Espero que os haya gustado esta explicación de la propiedad distributiva de la multiplicación desde el punto de vista geométrico y os haya servido de ayuda.
Y si quieres aprender muchas más matemáticas de primaria, adaptadas a tu nivel, regístrate en el método Smartick y pruébalo gratis.
Para seguir aprendiendo:
- Propiedad distributiva de la multiplicación
- Cómo realizar multiplicaciones con un modelo de área
- Propiedad conmutativa de la multiplicación y de la suma
- La propiedad distributiva de la multiplicación
- Aplicación de la propiedad distributiva
- ¿Cómo se hacen divisiones de 3 cifras? II - 04/09/2017
- Potencias: paréntesis y signos negativos - 17/10/2016
- ¿Cómo se hacen divisiones de 3 cifras? - 19/09/2016








Excelente, muy detallado, me encantó.
Excelente explicación. Me aclaró muchas dudas. Gracias
Muchas gracias a ti, Norma 🙂
Me encanta. se adquiere claridad en los conceptos de forma muy rápida
Buenas noches. Hace dos meses apunte a mis hijas a vuestro método por un año y estoy encantado. Me pregunto si no habrá un curso avanzado de matemáticas para adultos. Soy licenciado en empresariales y siempre me gustaron las asignaturas de ciencias y me gustaría volver a estudiar por placer. Un saludo y enhorabuena por vuestro metodo
Muchas gracias Carlos!
Nuestro método por ahora sólo llega hasta los 14 años, contenidos de 2º de la ESO.
Creo que no hay ningún otro método online igual de potente que el nuestro con contenidos para licenciados.
Soy ingeniero y el método que emplean me parece excelente para los niños en sus primeras etapas de estudio. Se necesitan tener ciertas habilidades y pedagogía para enseñar a los más pequeños. ¡Éxito!