El Método ABN constituye una de las innovaciones educativas más destacadas en las aulas españolas de Educación Primaria en el área de matemáticas en los 10 últimos años. Creado por Jaime Martínez Montero, ha alcanzado gran difusión a través de su blog, un canal de Youtube con multitud de vídeos de trabajo en aula, cursos de formación de profesores, los libros de Jaime Martínez (los últimos, con Concepción Sánchez Cortés), libros de texto, las Jornadas para el Aprendizaje y la Enseñanza de las Matemáticas (JAEM), los Congresos ABN. Se esperan novedades del método, como su extensión a Educación Infantil, en el próximo Congreso Iberoamericano de Educación Matemática (CIBEM, Madrid, 2017).
El Método ABN ha incorporado recursos conocidos en la enseñanza de las matemáticas, como la tabla 100, los palillos agrupados de 10 en 10, las monedas empleadas como ayuda para comprender el sistema de numeración decimal, o recursos online como el tutor ABN. Uno de sus mayores logros es haber creado un entorno innovador en el que todos estos recursos se integran de forma natural.
En esta entrada queremos mostrar, a través de un ejemplo, cómo son los algoritmos abiertos basados en números que dan nombre al Método ABN, en un contexto de invención de problemas.
La imagen siguiente, tomada de una clase de 3º del CEIP Virgen de Peña Sacra, de Manzanares el Real, muestra cómo se trabaja en clase la invención de problemas. A cada alumno se le proporciona un par de operaciones combinadas. Javier debe elaborar un problema que se resuelva primero restando 415 – 193 y después dividiendo el resultado entre 2. Posteriormente, deberá encontrar la solución a su propio problema.
Vemos que el enunciado requiere alguna modificación, como acabar preguntando “¿cuántos asientos hay en cada fila?”. Ponemos este ejemplo de trabajo de invención de problemas porque, más allá de los Algoritmos ABN, el Método ABN incorpora otros elementos innovadores como una mayor vinculación de los algoritmos con la resolución de problemas.
En la siguiente imagen, vemos el procedimiento que ha seguido Javier en la resta 415 – 193. El algoritmo se estructura en tres columnas. En la columna de la izquierda, ponemos las partes del sustraendo que vamos quitando: primero restamos 100, luego 90 y finalmente 3. En la columna central, aparece la parte del minuendo que va quedando tras las restas sucesivas. En la columna de la derecha, las partes del sustraendo aún pendientes por restar. Este algoritmo podría leerse por filas: Tengo que quitar 193 a 415. Primero quito 100, me quedan 315, y me falta por quitar 93; después, quito 90, tengo 225 y me faltan por quitar 3; finalmente, quito 3 y el resultado es 222.
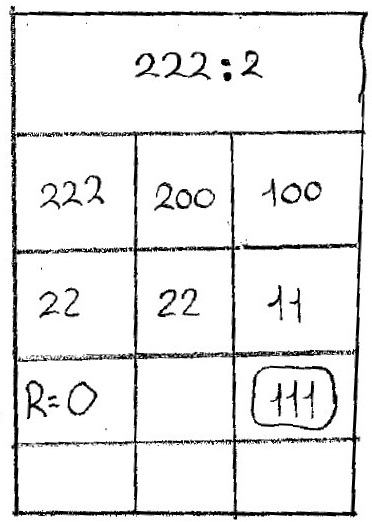
A continuación observamos el algoritmo ABN correspondiente a la división. En la columna de la izquierda figuran las partes del dividendo que van quedando hasta llegar al resto de la división. En la columna central se van poniendo las cantidades que se restan al dividendo. A la derecha, las cantidades que incorporamos al cociente. Podemos leer la división comenzando por la fila de arriba: Para dividir 222 entre 2, ponemos 100 en el cociente, que multiplicado por 2 da 200. Lo restamos a 222 y nos queda 22. Después multiplicamos 11 por 2 y restamos el resultado al 22 que queda en el dividendo, con lo que el resto es 0. Finalmente, sumamos las cantidades del cociente (100 y 11) y obtenemos el cociente de la división 111.
Lo que más llama la atención en estos algoritmos son sus grandes diferencias con los algoritmos tradicionales. Son algoritmos abiertos, de modo que cada estudiante los puede hacer de una forma distinta, adaptándose a su capacidad de cálculo y evolucionando a su propio ritmo en eficiencia; y están basados en números, porque las cifras no aparecen desprovistas de su valor posicional. Es decir, al restar las centenas no decimos “del 1 al 4, 3”, sino “415 menos 100 son 315”. Desaparece la dificultad de “la llevada” en la resta y empleamos un tipo de algoritmo más cercano e integrable con las estrategias de cálculo mental.
En un contexto escolar, en que los algoritmos parecían un elemento incuestionable, los algoritmos ABN han supuesto el cambio radical que ha removido el terreno y ha permitido implementar otras innovaciones didácticas menos audaces que, en conjunto, conforman el Método ABN.
Para seguir aprendiendo:
- Método alternativo para resolver una división
- Cómo resolver un ejercicio de división de decimales
- Cómo resolver un ejercicio de división de 2 cifras
- Cómo resolver un ejercicio de división por una cifra
- Aprende a dividir por una cifra
Fundador de la revista Edma 0-6: Educación Matemática en la Infancia. Miembro de la SEIEM.
Entusiasmado por la Educación Matemática en los primeros años. Cambiar la Educación Matemática es posible.
Muy buena entrada Carlos. Os invitamos a visitar la web de La Pandilla de la Rejilla con infinidad de contenido gratuito referente a la metodología de Algoritmos Abiertos ABN.
Un saludo
En pocas ocasiones me he encontrado con una explicación tan sucinta y, a la vez, tan completa como la que aquí haces sobre el método ABN. La suscribo. Muchas gracias.