En el post de hoy vamos a hablar de los fundamentos del Método Singapur.
Antes de nada, un poco de historia: Singapur es un país muy pequeño que carecía (y carece) de recursos naturales situado entre Malasia e Indonesia. En 1965 era una isla de pescadores y ahora tiene uno de los puertos con más tráfico del mundo, además de ser una de las ciudad-estado más prospera de Asia.
¿Cómo lo consiguió? Entre otras cosas, Singapur decidió apostar por la educación, emprendió una reforma educativa y convirtieron la educación en un pilar fundamental del país. Ahora encabezan sistemáticamente las clasificaciones internacionales de educación.
“Escuelas que piensan, nación que aprende”
Índice
Fundamentos del Método Singapur
Estos son los fundamentos del Método Singapur, del enfoque metodológico que se aplica para la enseñanza de las matemáticas en Singapur.
El aprendizaje en tres etapas (Jerome Bruner)
Introducen los diferentes conceptos a través de la progresión denominada CPA.
Durante el primer paso los alumnos deben utilizar materiales concretos, manipulativos y objetos de la vida cotidiana.
En la segunda etapa, los alumnos hacen representaciones pictóricas, como dibujos o imágenes, que le ayuden a resolver el problema.
En la tercera etapa, llegan a la comprensión abstracta del concepto trabajado.

Desarrollar la comprensión de concepto y aprendizaje de procedimientos en paralelo (Richard Skemp)
La comprensión instrumental (saber hacer) es la capacidad de realizar una operación (una división larga, o una división de fracciones).
La comprensión relacional (saber qué) es la capacidad para explicar el procedimiento.
Las matemáticas relacionales son más fáciles de recordar, aunque son más difíciles de aprender, sin embargo, las matemáticas instrumentales permiten proporcionar la respuesta correcta de manera más rápida que la que se consigue mediante un pensamiento relacional.
En el método de Singapur (y también en Smartick) estos dos tipos de comprensión siempre van unidos.
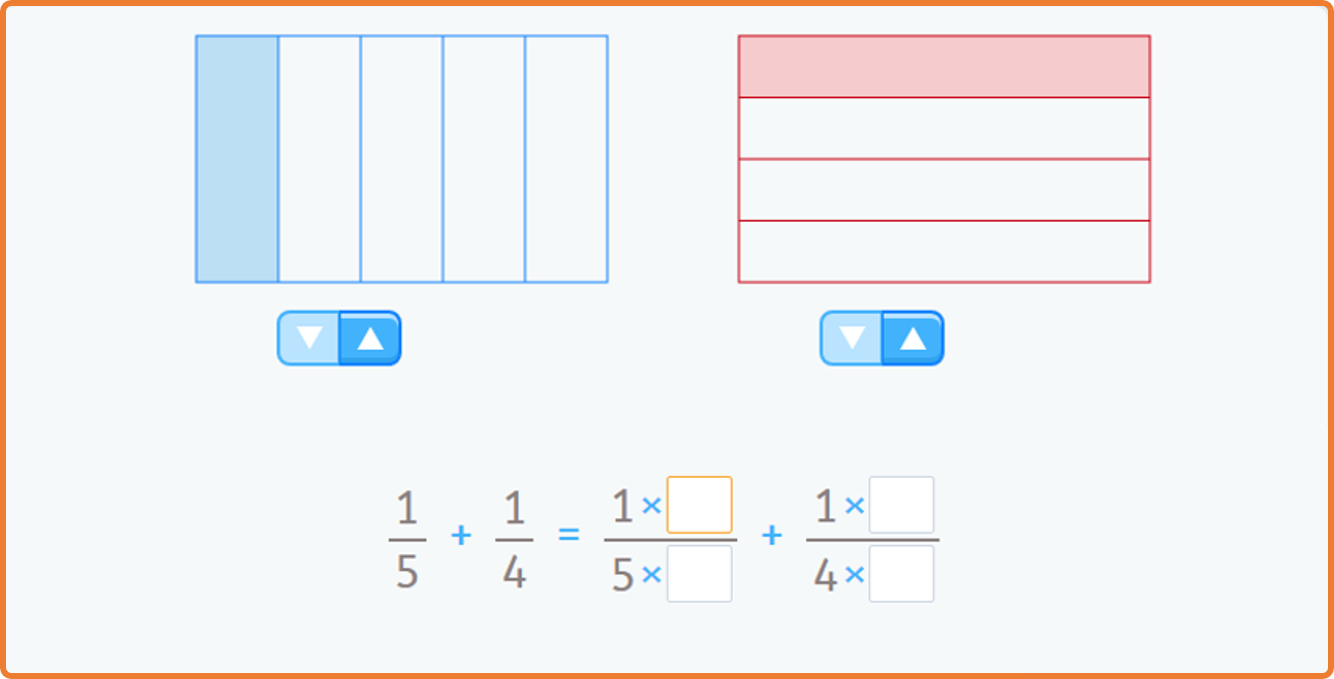
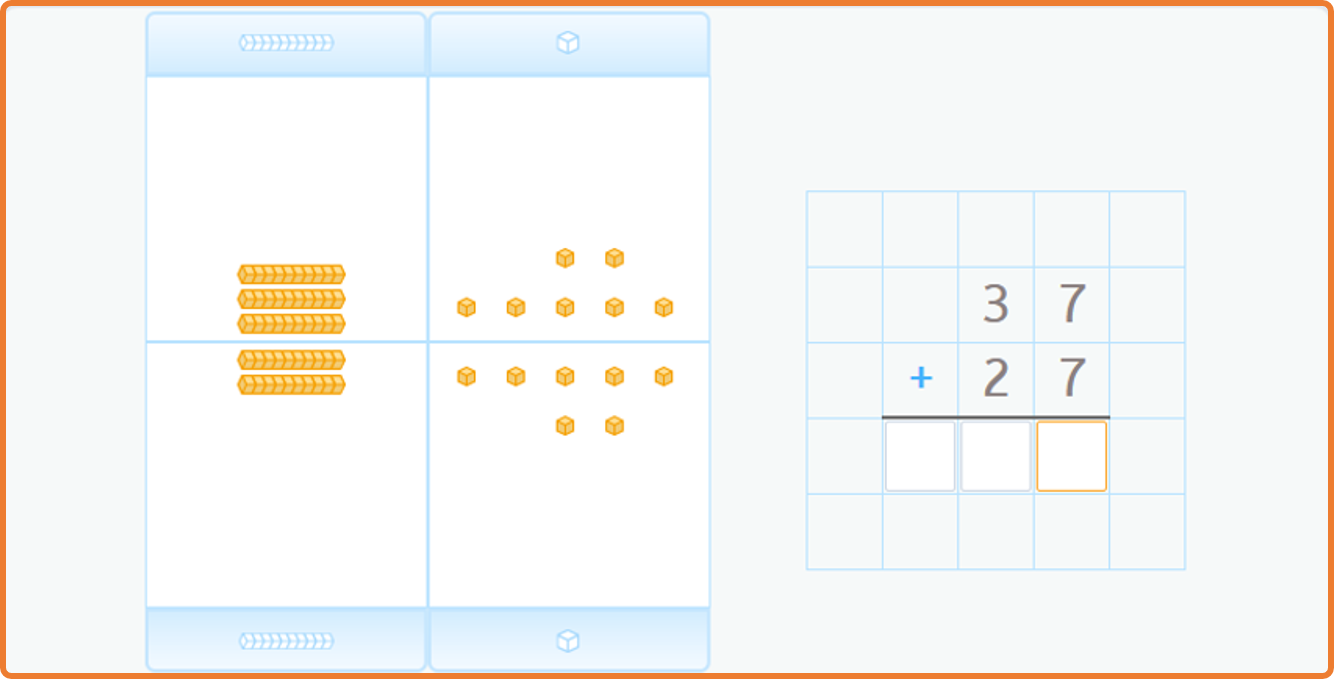
Variedad en las presentaciones (Zoltan Dienes)
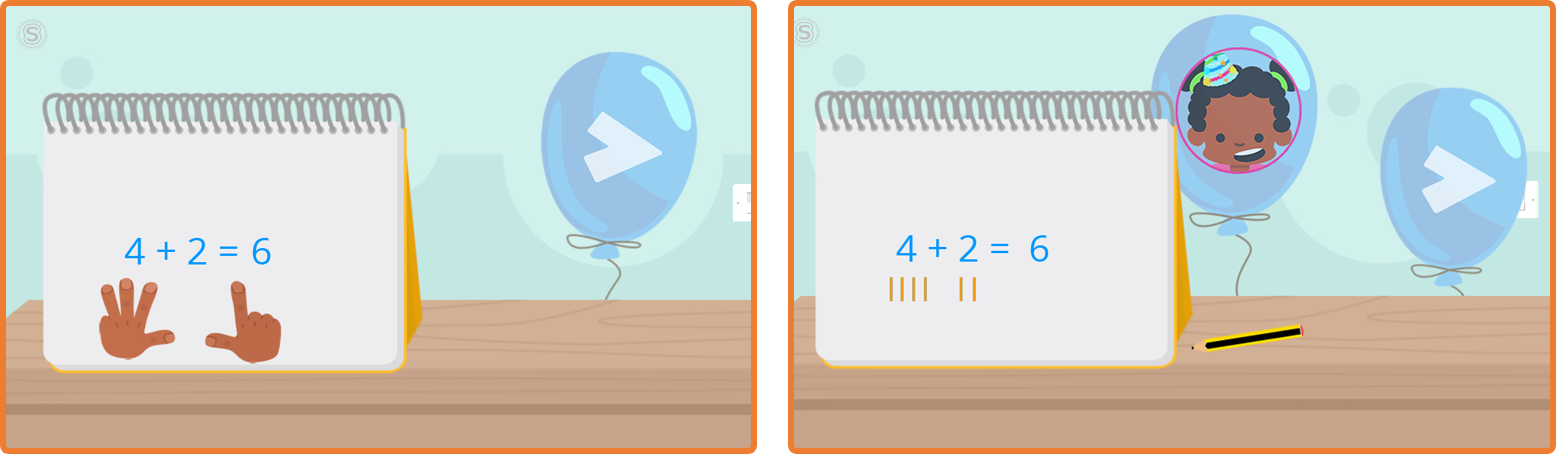
La comprensión de un concepto es mejor si se presenta desde distintos puntos de vista. Por ejemplo, para resolver una suma sin objetos podemos dibujar marcas y contarlas todas. Otra opción, sería resolverla con los dedos, poniendo en una mano 4 y en la otra 2 y contarlos todos.
El andamiaje y la zona de desarrollo próximo (Lev Vygotsky)
Los alumnos construyen su aprendizaje a través de interacciones que le ayudan a progresar de la zona de desarrollo actual (que representa lo que el alumno sabe) a la zona de desarrollo potencial (que representa lo que este puede llegar a saber).
A continuación, os muestro un ejemplo de secuencia didáctica de los que existen en Smartick.
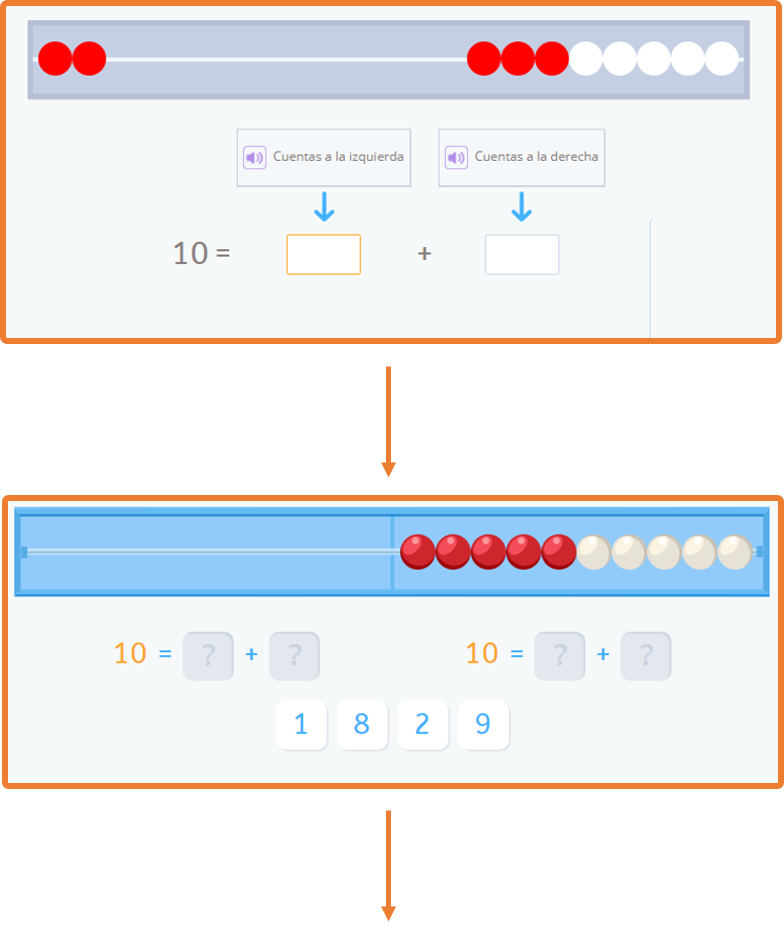
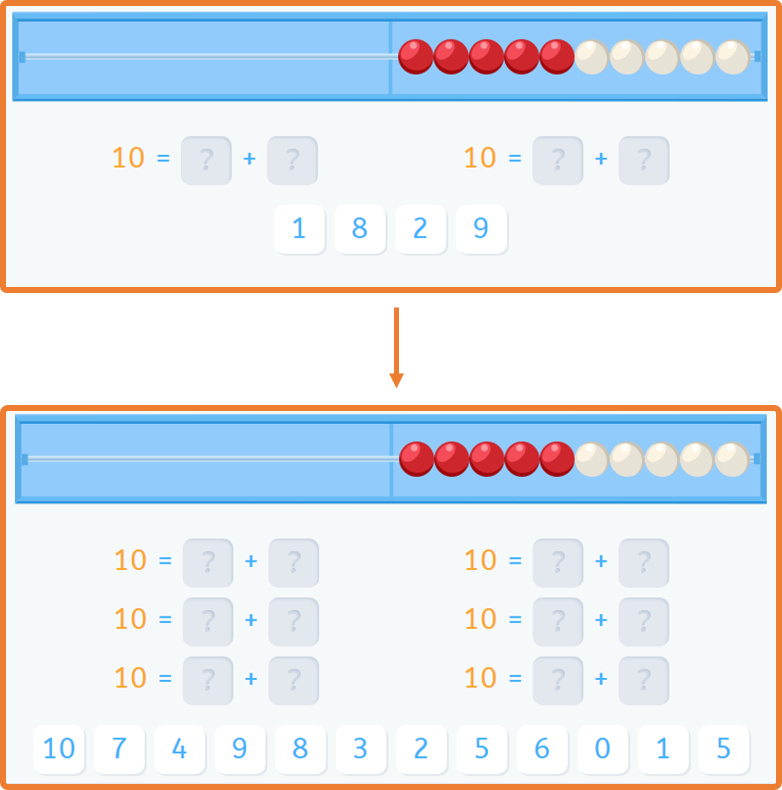
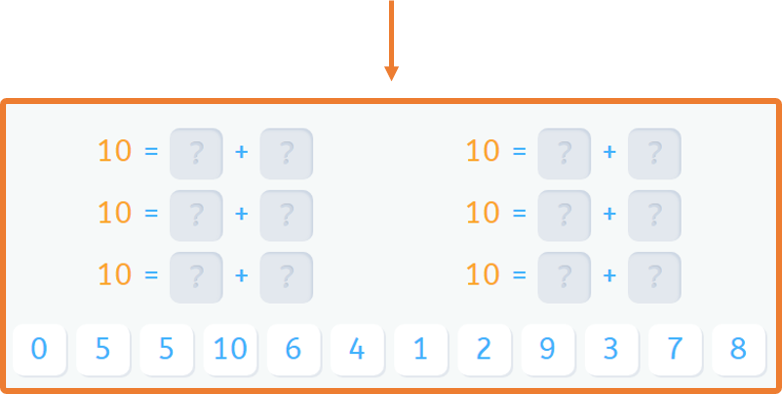
¿Te ha gustado este post sobre la explicación del Método Singapur? Si quieres seguir aprendiendo matemáticas, entra en Smartick y pruébalo gratis.
Para seguir aprendiendo:
- Singapur: Metas, objetivos y diseño de su Plan de Estudios
- Singapur: Principios de enseñanza y fases de aprendizaje
- Barras de Singapur aplicadas a la suma y resta
- Barras de Singapur aplicadas a la multiplicación de fracciones
- Singapur: Plan de estudios de matemáticas en primaria
- Resolución de problemas de matemáticas - 24/02/2020
- Las cinco etapas de la práctica deliberada - 06/01/2020
- La auto explicación en el proceso de aprendizaje - 25/11/2019








Muy interesante
ME PARECE UN METODO DE ENSEÑANZA MUY BUENO Y PRÁCTICO.
ME PARECE MUY INTERESANTE Y INFORMATIVO.
muy bueno
me parece excelente
Me parece un metódo muy interesante.
Es un excelente método, los niños aprenden jugando y haciendo.
Hola Jaime:
Muchas gracias por tu comentario.
Enseñamos matemáticas de la manera más divertida y práctica posible y los resultados en las notas del colegio nos avalan.
Estamos a tu disposición para cualquier duda que podáis tener en [email protected]
¡Un saludo!
Este método es muy interesante para los estudiante ya que siempre debemos realizar actividades con material concreto
Excelente y muy buena información
Soy docente argentina muuuuuy mayor!!! Me interesa el método. Estoy tratando de aprenderlo y aplicarlo con mis alumnos pequeños.
Buenos días
Soy una profe que está enseñando a los niños con el método singapur, piensa infinito de sm. Quisiera saber si smartick es compatible con este método. Me ha parecido que sí, pero me gustaría que me lo asegurárais.
Un saludo
Leyre
Hola Leyre, te han enviado un correo mis compañeras de atención pedagógica e la dirección que nos facilitas en el comentario. Respondemos también por aquí por si puede aclarar la duda a más personas.
Bajo nuestro nuestro punto de vista es compatible y apropiado estudiar diferentes algoritmos en la escuela como puede ser el método Singapur, o el método ABN, y el uso de los algoritmos que utilizamos en Smartick. Aprender más de un algoritmo para una operación es algo beneficioso para el aprendizaje de las matemáticas. Permite a un alumno mejorar su flexibilidad, pudiendo elegir el algoritmo que mejor se adapte al problema concreto que aborda, el que más domina, su preferido, etc.
Desde Smartick pensamos que los alumnos que estudian en los colegios en que se utilizan algoritmos alternativos a los tradicionales están en las mejores condiciones para aprender los algoritmos tradicionales y pueden beneficiarse mucho de este aprendizaje. La unión de los algoritmos alternativos con el estudio de los tradicionales contribuirá a un aprendizaje más completo de las operaciones aritméticas. También a una mejor comprensión de los algoritmos y a un mayor desarrollo del sentido numérico.
Disponemos de tutoriales interactivos que explican los algoritmos desde una comprensión de la realidad numérica que hay detrás de ellos. Estos tutoriales se proponen al alumno antes de enfrentarse por primera vez a las actividades relacionadas. Y también pueden realizarlos desde el colegio del mundo virtual después de la sesión.
Además, creemos en la importancia del uso flexible de los números. Y ofrecemos un escenario propicio para la práctica de estrategias de cálculo como las descomposiciones, elementos de convergencia de ambos métodos.
En resumen, creemos que es un contenido complementario que, lejos de entorpecer, enriquecerá su conocimiento matemático.
La mejor forma de conocer Smartick es probarlo en primera persona, por ello os animamos a registraros y trabajar en las sesiones gratuitas del periodo de prueba.
No dudes en contactarnos para cualquier consulta adicional en [email protected]
¡Un saludo!
Hola! Muy bueno! Me interesa , estoy enseñando con ese método. Sí es posible me envíes variedad de ejercitacion estaré muy agradecida
Quiero recibir información
Hola Andrea:
Paso tu correo a mis compañeras de atención pedagógica y a padres para que contacten contigo.
Puedes escribirles en todo momento a [email protected]
¡Un saludo!
Buenisima
ES UN MÉTODO MUY ÚTIL