Las matemáticas son un lenguaje universal que nos permite describir y comprender el mundo que nos rodea. Una de las ramas fundamentales de las matemáticas es el álgebra, y una herramienta clave en esta disciplina son las expresiones algebraicas. En este artículo, exploraremos qué son las expresiones algebraicas, para qué sirven y cómo se utilizan en el mundo real.
Las expresiones algebraicas aparecen como una de esas novedades en el paso de primaria a secundaria, sobre los 12 años de edad. Llegan con la enseñanza secundaria y lo hacen para quedarse. Como ocurre muchas veces con las novedades, las expresiones algebraicas son temidas y cuestionadas por los alumnos, por eso conviene empezar aclarando qué son y para qué sirven.
Índice
¿Qué son las expresiones algebraicas?
Las expresiones algebraicas son combinaciones de números, variables y operaciones matemáticas, como la suma, resta, multiplicación y división. Se representan mediante símbolos y letras, donde los números se consideran constantes y las letras representan variables, es decir, valores que pueden variar. Funcionan todas las reglas aritméticas que hemos aprendido hasta ahora, solo que algunos números son sustituidos por letras que pueden recibir distintos valores. Se va a entender mejor con ejemplos:
- Suma de dos números: Si tenemos dos números, por ejemplo, el 3 y el 5, sabemos que para sumarlos se escribe 3+5. Sabemos que su suma vale 8. Si los dos valores no son conocidos, también podremos sumarlos, aunque ahora no sabremos el resultado. Podemos representar esos dos números con las letras x e y, que como no tienen un valor fijo se llamarán variables. Si queremos expresar la suma de estos dos números, podemos usar la expresión algebraica: x + y. Observa que usamos dos variables distintas porque no nos han dicho que sean el mismo número, solo que queríamos obtener una expresión para la suma de «dos números».
- El doble de un número: 2x
- Área de un rectángulo: Al igual que para calcular el área de un rectángulo de base 4 y altura 2 multiplicamos 4 por 2, si deseamos calcular el área de un rectángulo con base «b» y altura «a», podemos utilizar la expresión algebraica: A = b · a, donde «A» representa el área del rectángulo.
- Fórmula del área de un círculo: Si conocemos el radio de un círculo, representado por «r», podemos utilizar la expresión algebraica: A = π · r2 para calcular su área. Aquí, «A» denota el área del círculo y π es una constante que representa el valor aproximado de pi, usualmente tomamos 3,1416.
- Conversión de temperatura: Supongamos que deseamos convertir una temperatura en grados Celsius a grados Fahrenheit. Podemos utilizar la expresión algebraica: F = (9/5) · C + 32, donde «C» representa la temperatura en grados Celsius y «F» representa la temperatura equivalente en grados Fahrenheit.
¿Para qué sirven las expresiones algebraicas?
Como ya habrás podido intuir por los ejemplos, las expresiones algebraicas se utilizan para describir situaciones y relaciones matemáticas en términos generales. Esto es, en situaciones en las que no todos los valores son conocidos. Nos permiten expresar fórmulas, ecuaciones y modelos matemáticos de manera abstracta, lo que facilita el análisis y la resolución de problemas.
Un ejemplo de la utilidad de las expresiones algebraicas sería, por ejemplo, obtener nuevas fórmulas. Como sabemos que el volumen de los prismas y los cilindros es el área de la base (Ab) por la altura (h) V = Ab· h, podremos sustituir en esa fórmula el área de la base. Si sabemos que la base es un círculo, Ab= π · r2 podremos sustituir y escribir en una sola fórmula que el volumen del cilindro es V = π · r2 · h.
Componentes de las expresiones algebraicas
- Constantes: Son números fijos que no cambian su valor, como 2, 5 o π.
- Variables: Son letras que representan cantidades desconocidas o variables, como x, y, z. Estas variables nos permiten generalizar y resolver problemas para diferentes valores.
- Operaciones matemáticas: Incluyen suma, resta, multiplicación, división y exponentes, entre otras. Estas operaciones se aplican a las constantes y variables para formar expresiones más complejas.
Lo que no se incluye en las expresiones algebraicas es la igualdad, los ejemplos que hemos visto antes que contenían el signo igual lo que tenían a la izquierda se interpreta como el resultado de esa expresión, cuando tengamos a la izquierda otra expresión, estaremos hablando de ecuaciones y lo tratamos al final del artículo.
Simplificación de expresiones algebraicas
Las expresiones algebraicas pueden simplificarse mediante el uso de propiedades y reglas algebraicas, como la distributiva, asociativa y conmutativa. La simplificación ayuda a reducir la expresión a una forma más manejable y comprensible. En el fondo, lo que se hace con el álgebra es extender cualquier regla aritmética, si vale para números, vale para expresiones algebraicas, x + x valdrá 2x.
Aplicaciones en el mundo real
Las expresiones algebraicas tienen numerosas aplicaciones en el mundo real. Algunos ejemplos incluyen:
- Física: En la descripción de leyes y fenómenos físicos, como la ley de gravitación universal o las ecuaciones del movimiento.
- Economía: En la modelización de problemas financieros, como el cálculo de intereses, beneficios o depreciación.
- Ingeniería: En el diseño y análisis de estructuras, circuitos eléctricos o sistemas de control.
- Ciencias de la computación: En algoritmos y programación, donde las expresiones algebraicas se utilizan para realizar cálculos y tomar decisiones.
Un caso particular, los monomios
Los monomios son un caso particular de expresiones algebraicas que solo utilizan la operación producto y en las que los exponentes de las variables que aparezcan tienen que ser números naturales (por tanto positivos). De las expresiones algebraicas vista en esta entrada serían monomios, todas menos esta dos: (9/5) · C + 32, además de x + y por contener una suma- Tampoco lo sería 1/x porque escrito como potencia es x-1, que no es un número natural.
Puedes ver más información sobre monomios en la entrada que hicimos en el blog sobre ellos. Incluimos un vídeo, que es uno de nuestros tutoriales interactivos convertido en vídeo, por lo que deja de ser interactivo 🙁. Aún así tiene la gran ventaja de que se puede visualizar tantas veces como sea necesario y compartir. Si quieres acceder a los tutoriales interactivos de verdad, puedes hacerlo registrándote en Smartick, el método online de aprendizaje de matemáticas para niños de 4 a 14 años.
Expresiones algebraicas y ecuaciones
Entre las aplicaciones no hemos citado una de las principales, porque merece un epígrafe entero, que es el de las ecuaciones. Las ecuaciones no son expresiones algebraicas, por poco, porque lo que son es dos (o más) expresiones algebraicas unidas por el signo igual. Se va a entender mejor, como todo, con un ejemplo:
Decíamos arriba que el doble de un número es 2x. ¿Cómo diríamos «un número es el doble de otro»? No puede ser x = 2x, porque eso sería un número es igual a su doble. Pero sí puede ser y = 2x, porque al usar dos variables (letras) distintas estamos denotando exactamente eso. Si, por ejemplo consideramos los pares de puntos (x,y) que cumplen esa ecuación, esa igualdad entre expresiones algebraicas, tendríamos el (1,2), el (10,20), el (π, 2π) y TODOS los pares en los que la segunda coordenada es el doble que la primera. Podemos incluso pintarlo, tomando, como se suele tomar, la primera coordenada en el eje x y la segunda en el y:
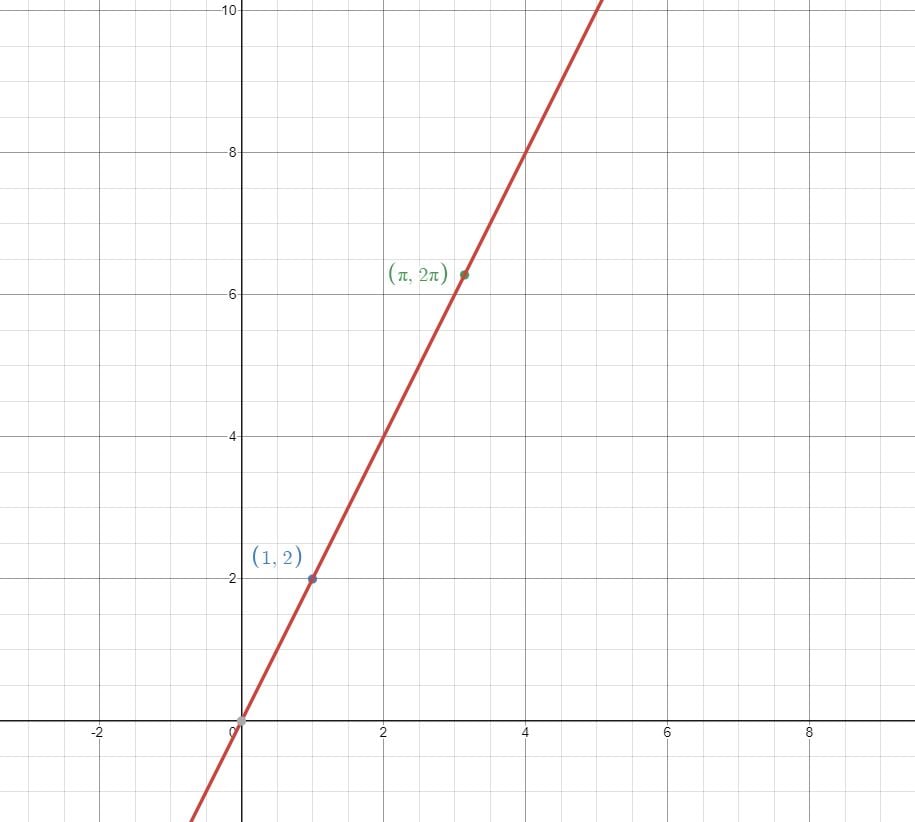
Estirando «un poco» la idea podríamos intentar pintar la siguiente ecuación, que no deja de ser una igualdad entre expresiones algebraicas, eso sí, mucho más difícil de traducir con palabras:
Puedes probar a cambiar alguno de los valores de la expresión en la potente calculadora gráfica desmos.
Espero que la entrada te haya resultado interesante, no dudes en compartirla o en escribir en comentarios tus dudas o cuestiones, o los temas de los que te gustaría saber más. Para aprender más, registrate en Smartick, el método online de aprendizaje de matemáticas y comprensión lectora para niños de 4 a 14 años.
Para seguir aprendiendo:
- Fórmulas matemáticas: Qué son, cómo se componen y tipos de fórmulas
- Las propiedades de los monomios
- Funciones matemáticas: ¿sabes lo que son?
- Introducción a las ecuaciones
- Estrategia para multiplicar por 2, por 4 y por 8
Es formador de maestros, tanto en formación inicial en la Facultad de Educación de la Universidad Complutense de Madrid como en formación continuada. Apasionado de tocar las matemáticas.
Forma parte del equipo de Didáctica de Smartick.
Autor del blog Tocamates y del libro “Y me llevo una”.
Le encanta la divulgación y -en general- la comunicación. No calla ni debajo del agua, de ahí que colabore con varias radios y medios de comunicación, y que si tiene un rato, se eche unos largos en la piscina.
- El lenguaje de funciones y gráficas - 14/02/2024
- Cómo aplicar la jerarquía de operaciones - 20/09/2023
- Expresiones algebraicas: ¿Qué son? ¿Para qué sirven? - 21/07/2023
¿En qué año se publicó este articulo?
¡Hola, Jesús! Este post se publicó en el 2023. ¡Un saludo! 😊
Gracias, muy interesante.
¡Hola, Jorge! Esperamos que te haya servido de ayuda nuestro post. 😊