Las funciones matemáticas son como máquinas mágicas matemáticas que nos ayudan a relacionar números de una manera especial. Imagina que las funciones son como recetas secretas que toman un número y hacen algo interesante con él. Dentro de una función matemática hay combinaciones de números, variables y operaciones matemáticas, como la suma, resta, multiplicación y división, es decir, expresiones algebraicas.
Índice
¿Qué es una función?
Una función es como una regla que nos dice qué hacer con los números. En matemáticas, escribimos una función como f(x) o y = f(x) para mostrar que está relacionada con un número al que llamamos x. Podemos utilizar otra letra para representar este número. Si usamos la letra m la función se escribiría como f(m) o si usamos la letra p, la función se escribiría como f(p).
Cuando ponemos un número en la función, obtenemos otro número como resultado. ¡Vamos a ver un ejemplo!
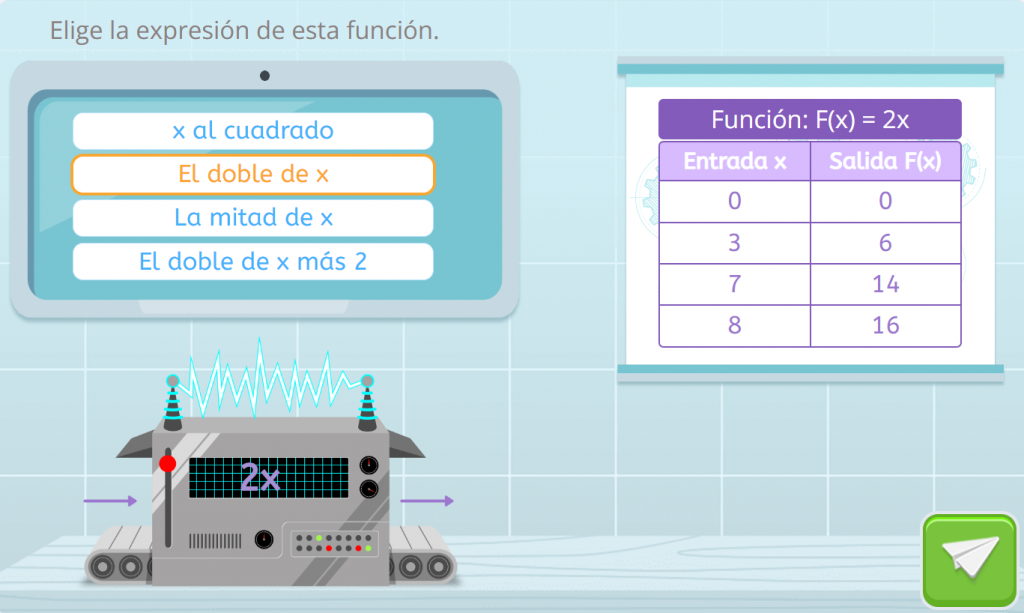
En este ejercicio de Smartick tenemos una máquina que hace que cualquier número que entre se transforme en el doble porque lo multiplica por 2. Por ejemplo, si metemos el número 3 en la máquina, ¡obtenemos 6! Entonces, «doble(3)» es igual a 6. Esta es la función doble.
¿Puedes adivinar qué hace la función «mitad»? La función «mitad» es una función matemática que realiza una operación muy simple: toma un número y lo divide entre 2. En otras palabras, si metes un número x en la función «mitad,» obtendrás la mitad de ese número como resultado. Por ejemplo, si pones el número 8 en la función «mitad,» obtienes 4.
Ahora bien, en la matemática más formal, una función se define como una relación entre dos magnitudes variables. Esto significa que a cada valor de la primera magnitud, que en nuestro caso llamamos x, le corresponde un único valor de la segunda magnitud, que es su imagen.
La variable que consideramos en primer lugar es la variable independiente. La otra variable recibe el nombre de variable dependiente porque su valor depende del que haya tomado la primera.
Una función f entre las variables x e y se expresa de la siguiente forma:
y = f(x)
f(x) es la imagen de x, es decir, el valor que le corresponde a x por la función f.
Funciones matemáticas lineales
Este tipo de funciones matemáticas tienen la forma f(x) = mx + n donde:
- m es la pendiente de la gráfica de la función. Cuanto mayor es la m más inclinada es la recta de la gráfica.
- n es la ordenada al origen que es el valor de y cuando es igual a 0.
También reciben el nombre de funciones de proporcionalidad directa porque expresan una relación en la que las variables cambian en la misma proporción, lo que es una característica clave de este tipo de funciones matemáticas.
Ejemplo:
y = 2x + 3
Es una función lineal donde la pendiente es 2 y la ordenada al origen es 3. La gráfica de esta función es una línea recta que pasa por el punto (0, 3) y tiene una pendiente de 2. Más adelante, en este mismo post, veremos cómo representar funciones matemáticas.
Hay otro tipo de funciones matemáticas como las cuadráticas que tienen la forma f(x) = ax²+ bx + c o las funciones constantes que tienen la forma f(x) = c, donde c es una constante. Te invito a que descubras más tipos como las funciones de valor absoluto, exponenciales, logarítmicas y trigonométricas entre otras.
¿Cómo se representan las funciones matemáticas?
La gráfica de una función matemática es la representación en unos ejes de coordenadas de todos los pares (x,y), siendo x un valor de la variable independiente e y el correspondiente valor de la variable dependiente.
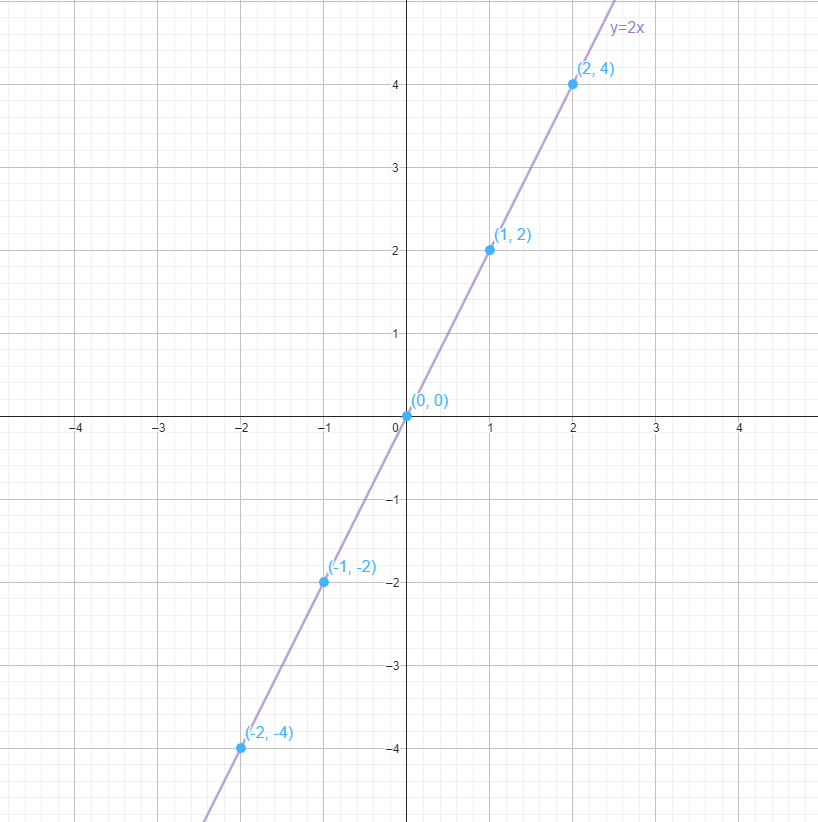
Para representar una función tenemos que seguir varios pasos. Por ejemplo, vamos a representar la función «doble» que es una función matemática lineal con pendiente 2:
y = 2x
- Dibuja un eje de coordenadas: Comienza dibujando un par de ejes perpendiculares en un papel. Un eje será el eje horizontal (llamado eje x) y el otro será el eje vertical (llamado eje y).
- Marca los puntos en los ejes: En el eje horizontal (eje x), etiqueta los valores que quieras representar. Podemos marcar los siguientes: -4, -3, -2, -1, 0, 1, 2, 3 y el 4. En el eje vertical (eje y), haz lo mismo. Recuerda que debe haber la misma distancia entre los puntos.
- Haz una tabla de valores de la función: La ecuación y = 2x nos dice cómo relacionar el valor de x con el valor de y. Para encontrar puntos en la gráfica, elige varios valores de x y calcula los correspondientes valores de y :
- Si x=-2 entonces y=2(-2)=-4. Obtenemos el punto (-2, -4).
- Si x=-1 entonces y=2(-1)=-2. Obtenemos el punto (-1, -2).
- Si x=0 entonces y=2(0)=0. Obtenemos el punto (0, 0).
- Si x=1 entonces y=2(1)=2. Obtenemos el punto (1, 2).
- Si x=2 entonces y=2(2)=4. Obtenemos el punto (2, 4).
- Dibuja los puntos: En el gráfico, coloca un punto en cada una de las coordenadas que encontraste en el paso anterior.
- Dibuja la recta que pasa por los puntos: Ahora, conecta los puntos que has dibujado con una línea recta. La línea pasará a través de todos los puntos que calculaste y representará la función y = 2x.
- Etiqueta la gráfica: Añade un título a tu gráfico y = 2x.
Para representar funciones matemáticas podemos utilizar la calculadora gráfica de GeoGebra o Desmos. Puedes elegir la que más te guste.
Ejercicio de funciones matemáticas lineales aplicado a la vida real
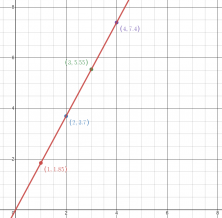
En la frutería de Leo el kilogramo de naranjas tiene un precio de 1,85 euros. Responde a las siguientes preguntas:
- Elabora una tabla de valores que relacione la cantidad de naranjas con su precio.
- ¿Son proporcionales los kilogramos de naranjas que se compran y el precio?
- Haz la gráfica de la función obtenida.
Solución al ejercicio propuesto
- Elabora la tabla de valores que relaciona la cantidad de naranjas con su precio.
| x | y |
|---|---|
|
1
|
1,85
|
|
2
|
3,7
|
|
3
|
5,55
|
|
4
|
7,4
|
- ¿Son proporcionales los kilogramos de naranjas que se compran y el precio?
- Sí, los kilogramos de naranjas que se compran y el precio son proporcionales en este caso. La razón es que el precio por kilogramo de naranjas es constante (1,85 euros por kilogramo). Esto significa que si duplicas la cantidad de naranjas (por ejemplo, de 2 a 4 kilogramos), el precio también se duplicará. Esta relación constante indica proporcionalidad directa.
- Haz la gráfica de la función obtenida.
Espero que la entrada te haya resultado interesante, no dudes en compartirla o en escribir en comentarios tus dudas o cuestiones, o los temas de los que te gustaría saber más. Para aprender más, registrate en Smartick, el método online de aprendizaje de matemáticas y comprensión lectora para niños de 4 a 14 años.
Para seguir aprendiendo:
- Cuarta parte
- Barras de Singapur aplicadas a la resolución de ecuaciones algebraicas I
- Líneas rectas, segmento y líneas semirrectas
- El valor posicional de los números
- El lenguaje de funciones y gráficas
Es además monitora de ocio y tiempo libre.
Forma parte del equipo de didáctica de Smartick, le gusta transmitir conocimientos y valores a los demás y aprender.
Siente curiosidad por lo desconocido, le encanta pasar tiempo con sus seres queridos y viajar.
Muchas, muchas pero muchas gracias por su explicación agradezco su aporte y felicidades ya que este tipo de información me ha servido muchísimo. SALUDOS DESDE MÉXICO.
Excelente explicación y las gráficas muy entendibles y oportunas, para poder tener una visión perfecta de la materia.
¡Hola, Agustín Emilio! Muchas gracias por tu comentario, esperamos que te haya servido de ayuda nuestro post. ¡Un saludo! 😊