En el post de hoy veremos qué son las identidades notables y algunos ejemplos. Las identidades notables son muy útiles en matemáticas porque nos ayudan a simplificar expresiones complicadas y a resolver problemas de forma más fácil. También son valiosas para la factorización de polinomios y la resolución de ecuaciones, facilitando el análisis y la comprensión de relaciones matemáticas. Estas fórmulas son fundamentales en el aprendizaje y la aplicación de conceptos avanzados en diversas ramas de las matemáticas.
Índice
Identidades notables
Las identidades notables o productos notables son resultados de multiplicar binomios que se pueden obtener directamente sin realizar la multiplicación. Su memorización es útil para abreviar los cálculos con expresiones algebraicas lo que permite simplificar y trabajar con estas expresiones de manera más fácil. Nos harán ganar mucho tiempo al momento de ejecutar la solución de un problema.
Formula identidades notables
Hay varias igualdades de gran importancia en matemáticas que se deben de aprender a manejar con soltura:
Cuadrado de una suma
El cuadrado de una suma de dos sumandos es igual al cuadrado del primer sumando, más el doble del primero por el segundo, más el cuadrado del segundo.
(a+b)² = a² + 2ab +b²
Ejemplos:
- (x + 3)² = x² + 2·x·3 + 3² = x² + 6x + 9
- (2 + 5x)² = 2² + 2·2·5x + (5x)² = 4 + 20x + 25x²
Cuadrado de una diferencia
El cuadrado de una diferencia es igual al cuadrado del primer sumando, menos el doble del primero por el segundo, más el cuadrado del segundo.
(a-b)² = a² – 2ab +b²
Ejemplos:
- (x – 5)² = x² – 2·x·5 + 5² = x² – 10x + 25
- (3 – 3x)² = 3² – 2·3·3x + (3x)² = 9 – 18x + 9x²
Suma por diferencia
La suma de dos monomios por su diferencia es igual a la diferencia de sus cuadrados.
(a+b)(a-b) = a² – b²
Ejemplos:
- (x + 5)·(x – 5) = x² – 5² = x² – 25
- (3 – 5x)·(3 + 5x) = 3² – (5x)² = 9 – 25x²
Si quieres, puedes comprobar los resultados de todos los ejemplos haciendo los productos.
Muchas veces nos llevan a cometer errores a la hora de hacer cálculos con ellas por eso es importante no memorizar simplemente las fórmulas sino intentar ver de dónde vienen.
Vamos a ver, desde el punto de vista geométrico, en qué consiste elevar al cuadrado la suma de dos cantidades (en nuestro caso a y b) para llegar a la primera de las fórmulas de las identidades notables que hemos puesto arriba.
Primero, vamos a ver cómo calcular el cuadrado de la suma de dos cantidades a y b, (a+b)².
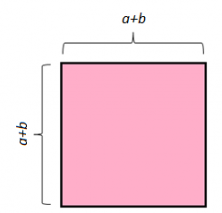
Construimos un cuadrado de lado a+b unidades:
Si calculamos el área de este cuadrado (sabemos que el área de un cuadrado es lado por lado), nos da: (a+b) × (a+b) que sería lo mismo que (a+b)² unidades al cuadrado.
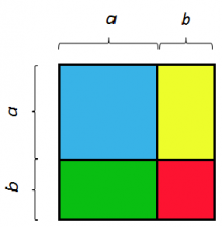
A continuación vamos a dividir el cuadrado en cuatro partes:
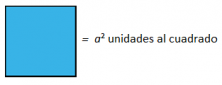
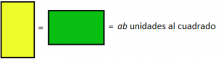
Nos salen dos cuadrados (azul y rojo) y dos rectángulos (verde y amarillo). Calculamos las áreas de cada figura:
Es fácil darse cuenta de que el área del primer cuadrado rosa de lado a+b, ((a+b)²), es la suma de las áreas del cuadrado azul (a²), del rojo (b²) y de los dos rectángulos iguales amarillos y verdes (2ab).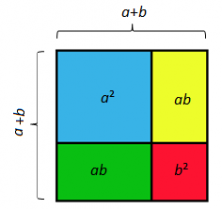
Por lo tanto, podemos ver que (a+b)² = a² + 2ab +b².
Lo mismo podremos hacer elevando al cuadrado la resta de dos cantidades y la multiplicación de la suma por diferencia. ¡Intenta hacerlo tú mismo, seguro que te sale!
Identidades notables ejercicios
En las sesiones de Smartick hay varios ejercicios para practicar las identidades notables, vamos a ver algunos ejemplos.
- Ejercicio 1. Cuadrado de una suma.
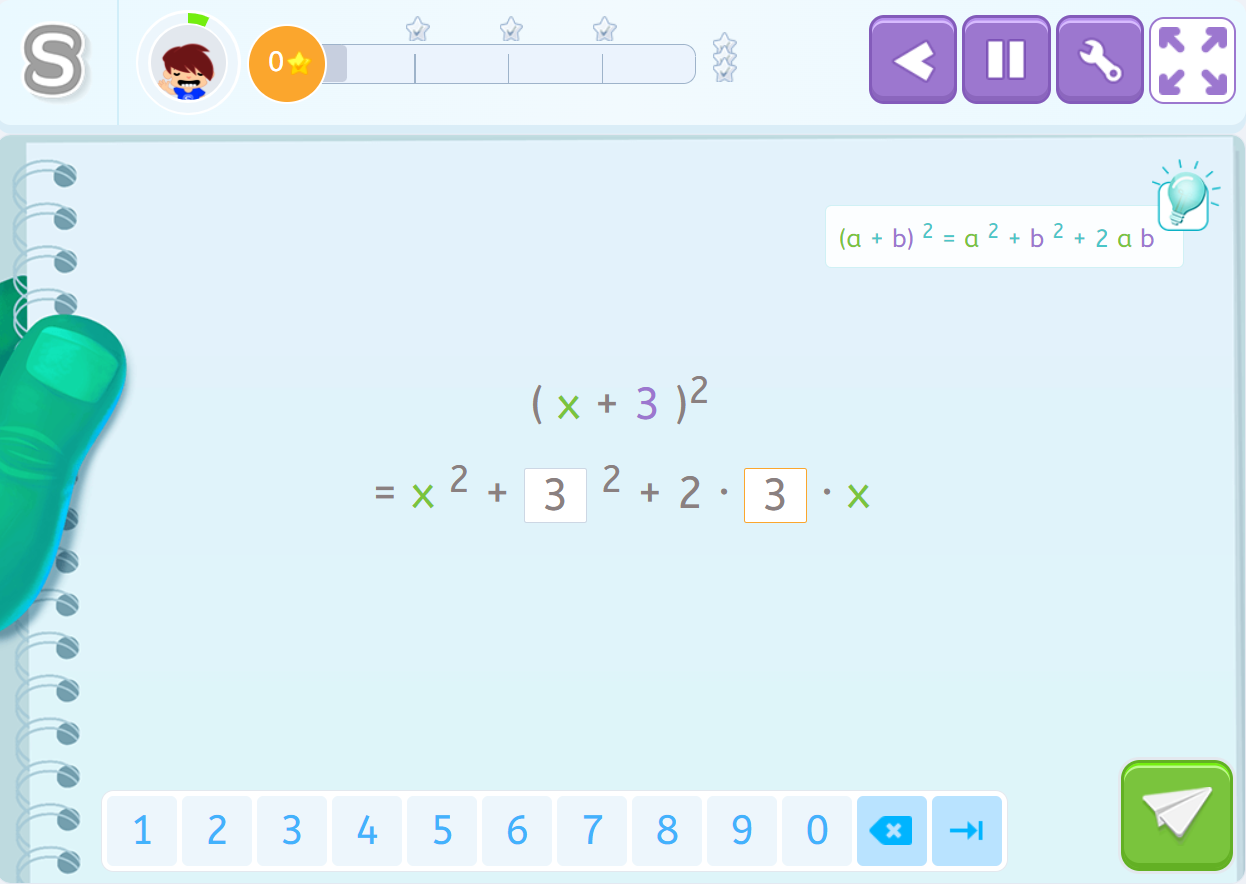
- Ejercicio 2. Cuadrado de una resta.

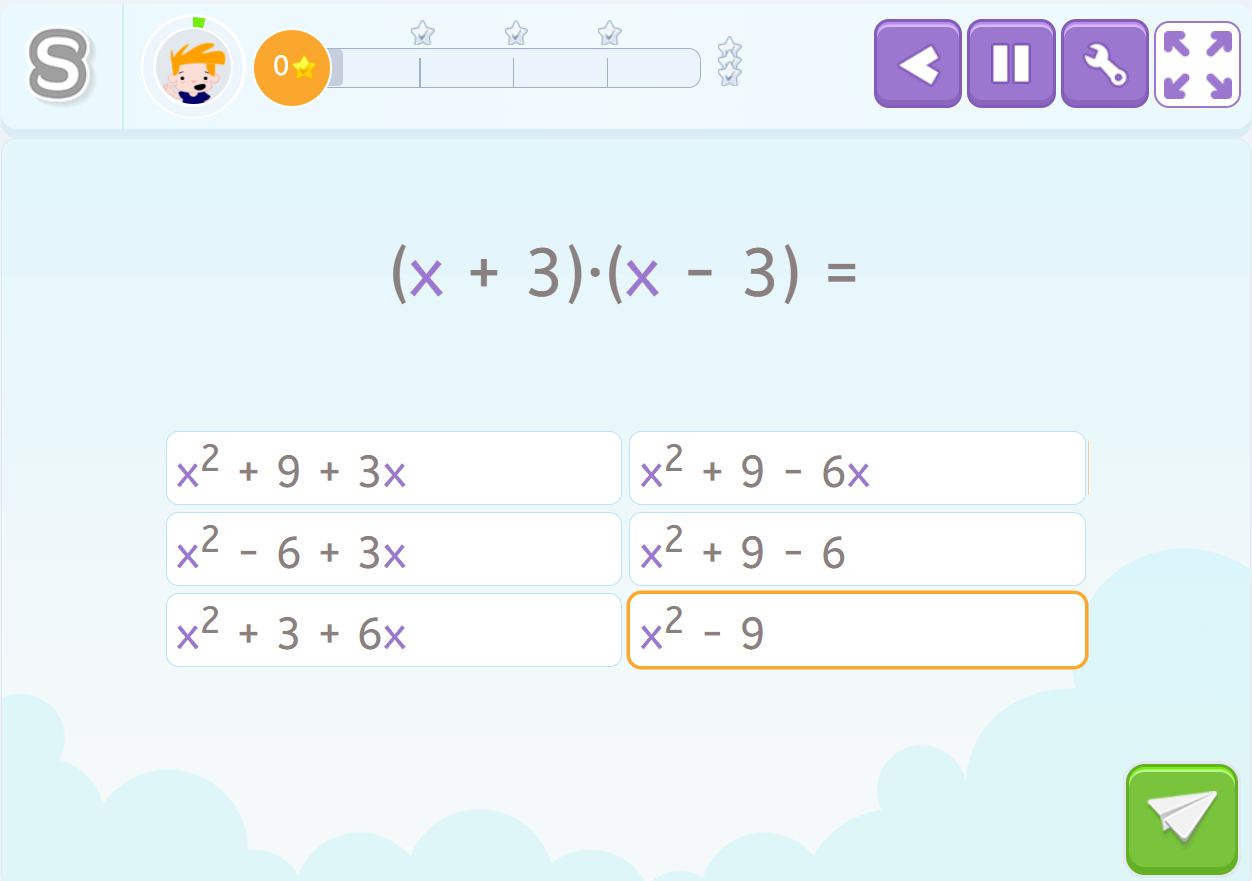
- Ejercicio 3. Suma por diferencia.
Las identidades que hemos visto en este post son fundamentales para simplificar y resolver problemas algebraicos, ya que permiten transformar expresiones complicadas en formas más simples y manejables. Son herramientas básicas en el aprendizaje y aplicación de conceptos matemáticos, especialmente en álgebra y cálculo.
Recuerda que en Smartick podrás practicar ejercicios de identidades notables, ¡y mucho más!
Para seguir aprendiendo:
- Cuadrado de un número
- Trucos para calcular el cuadrado de un número
- Perímetro: qué es y cómo calcularlo en cada figura
- Suma de números decimales
- Repaso de sumas en vertical con varios ejemplos
- ¿Cómo se hacen divisiones de 3 cifras? II - 04/09/2017
- Potencias: paréntesis y signos negativos - 17/10/2016
- ¿Cómo se hacen divisiones de 3 cifras? - 19/09/2016