¡Domina el arte de resolver ecuaciones! 🎯✏️
En este post vamos a ver que las ecuaciones son una parte fundamental de las matemáticas, ¡y no son tan difíciles como parecen! 😊 Vamos a hablar un poco sobre cómo resolver ecuaciones, algunos tips para hacerlas más sencillas y reconocer cuándo una expresión matemática se considera una ecuación.
Índice
¿Qué es una ecuación?
Una ecuación es una expresión matemática donde dos cosas son iguales. Se representa con un signo igual (=), y el objetivo es encontrar el valor que hace que ambos lados de la ecuación sean iguales.
Por ejemplo: 2x + 3 = 7
Pero primero vamos a ver qué pasos debemos seguir para resolverlas:
- Identifica la incógnita: Normalmente usamos letras como x o y para representar un valor desconocido.
- Despeja la incógnita: El objetivo es dejar sola a la incógnita en un lado de la ecuación. Para ello, usa operaciones inversas (sumar, restar, multiplicar o dividir) en ambos lados de la ecuación.
- Comprueba tu respuesta: Sustituye el valor que obtuviste en la ecuación original para ver si es correcto.
¡No te preocupes! Vamos a empezar por introducir ecuaciones sencillas. Pero antes de empezar recuerda realizar las mismas operaciones en ambos lados del signo igual. ¡Así mantienes el equilibrio y te aseguras de encontrar la solución correcta! Mira estos ejemplos:
- Suma y resta: x + 5 = 10 Para resolver, resta 5 en ambos lados ⇾ x = 5
- Multiplicación y división: 4x = 20 Divide entre 4 ⇾ x=5
Tipos de ecuaciones
En las enseñanzas obligatorias se ven ecuaciones de primer grado en el tránsito de primaria a secundaria, ecuaciones de segundo grado en secundaria y también sistemas de dos o más ecuaciones, generalmente de primer grado. No obstante, existen muchos otros tipos de ecuaciones como las ecuaciones exponenciales, logarítmicas, diferenciales o en derivadas parciales que se verán en cursos superiores.
Ecuaciones de primer grado
Son ecuaciones en las que la incógnita (generalmente representada por x) aparece con exponente 1. Tienen la forma: ax + b = 0. Donde a y b son números. Se llaman «lineales» porque su gráfica es una línea recta. Para resolverlas, solo necesitas despejar x.
Ecuación: 3x – 5 = 0
Suma 5 en ambos lados ⇾ 3x = 5
Divide entre 3 ⇾ \( \large \frac{5}{3} \)
Ecuaciones de segundo grado
Son ecuaciones donde la incógnita aparece elevada al cuadrado (exponente 2). Tienen la forma: ax² + bx c = 0. Donde a, b, y c son números. Estas ecuaciones pueden tener hasta dos soluciones, y su gráfica es una parábola. Se resuelven usando métodos como factorización, fórmula general o completando el cuadrado.
Para diferenciarlas podemos decir, las ecuaciones de primer grado tienen solo una solución y su gráfica es una línea recta y las ecuaciones de segundo grado pueden tener hasta dos soluciones y su gráfica es una parábola.
Cómo resolver ecuaciones de primer grado
- Simplifica ambos lados de la ecuación: Si hay términos semejantes (como números o términos con x) en un lado de la ecuación, combínalos.
- Agrupa las incógnitas en un lado y los números en el otro: Si x está en ambos lados de la ecuación, mueve los términos con x a un lado y los números al otro.
- Resuelve para x: Una vez que los términos con x estén aislados en un lado, despeja x dividiendo por el coeficiente que acompaña a x.
- Verifica la ecuación sustituyendo x por el resultado.
Cómo resolver ecuaciones de segundo grado
Fórmula general (o fórmula cuadrática)
La fórmula general para resolver cualquier ecuación cuadrática es:
\( \huge x=\frac{-b \pm \sqrt{b^2-4ac}}{2a} \)
El término dentro de la raíz cuadrada, b² − 4ac, se llama discriminante y determina el número de soluciones que tiene la ecuación:
- Si el discriminante es positivo (b² −4ac > 0), hay dos soluciones reales distintas.
- Si el discriminante es igual a cero (b² − 4ac = 0), hay una única solución real.
- Si el discriminante es negativo (b² − 4ac < 0), hay dos soluciones complejas.
Factorización
Algunas ecuaciones cuadráticas se pueden resolver factorizando, es decir, reescribiendo la ecuación como el producto de dos binomios.
Por ejemplo, la ecuación: x² − 5x + 6 = 0
Buscamos dos números que multiplicados den 6 (el término constante) y sumados den 5 (el coeficiente de x). Estos números son 2 y 3, por lo que podemos factorizar: (x−2)(x−3)=0.
Problemas de ecuaciones
Un tercio de las macetas que tiene Cecilia en su casa contienen margaritas, la mitad están llenas de pensamientos y las doce restantes tienen amapolas. ¿Cuántas macetas con flores tiene Cecilia en su casa?
Para poder resolverlo hay que transformar el enunciado en una expresión matemática. La incógnita, lo que tenemos que calcular (x), es en este caso el número de macetas.
- Empezamos fijándonos en la primera parte del enunciado: Un tercio de las macetas que tiene Cecilia en su casa contienen margaritas.
La x representa el total de macetas que tiene Cecilia. Es decir, lo que queremos averiguar. Sabemos que un tercio del total de macetas, sea este el número que sea, son margaritas.
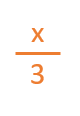
- Seguimos analizando el enunciado: la mitad están llenas de pensamientos.
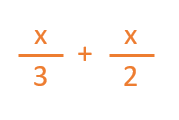
Hemos añadido otro término a la expresión. Ahora sabemos también que la mitad del total de macetas, sea este el número que sea, son pensamientos.
- Y acabamos utilizando el último dato que nos facilita el enunciado: las doce restantes tienen amapolas.
Por lo tanto, el número total de macetas que tiene Cecilia en su casa (x) se representaría con la siguiente expresión matemática:
Ahora vamos a resolver nuestra ecuación.
Lo primero que hay que hacer es poner un denominador común para todos los elementos de la fracción. Puedes recordar aquí cómo hacer sumas de fracciones con distinto denominador.
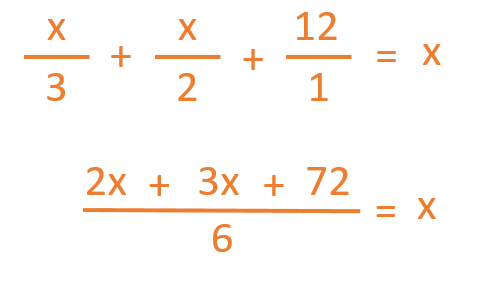
Luego debemos cambiar el denominador (6) de lado de la igualdad. Para ello, le cambiamos su rol, pasa de dividir en la parte izquierda de la ecuación a multiplicar en la parte derecha.
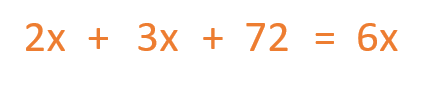
Ahora vamos a poner todas las incógnitas en el mismo lado del igual y todo lo que no es incógnita al otro lado del igual. Para ello cambiamos el 2x y el 3x al lado opuesto y por eso le cambiamos el signo.
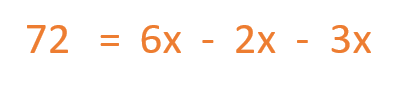
Después operamos con las distintas incógnitas 6 – 2 – 3 = 1
Por tanto, el resultado final es:
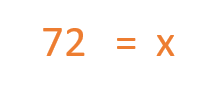
Ahora ya sabemos que Cecilia tiene 72 macetas.
Para comprobar si es correcto, solo tienes que revisar si se cumplen todas las condiciones.
- Un tercio, 24, son margaritas.
- La mitad, 36, son pensamientos.
- Y 12 son amapolas.
24 + 36 + 12 = 72
¡Eso es, todo correcto! Si quieres seguir aprendiendo sobre las ecuaciones, puedes visitar el blog de Smartick y consultar ¿Cómo se resuelven los problemas de ecuaciones?
Esperamos que la entrada haya sido de tu agrado, y si quieres seguir practicando matemáticas adaptadas a tu nivel, regístrate en Smartick y pruébalo gratis.
Para seguir aprendiendo:
- Ecuaciones reducibles: ¿qué son? ¿cómo se resuelven?
- ¿Cómo se resuelven los problemas de ecuaciones?
- Barras de Singapur aplicadas a la resolución de ecuaciones algebraicas I
- Fracciones con una incógnita
- Balanzas en matemáticas: ¿Qué son y para qué se utilizan?
Maestro de vocación y acción, forma parte del departamento de pedagogía de Smartick y trata de aportar la experiencia que ha ganado curso tras curso en el aula.
Cree ciegamente que no hay mejor forma de enseñar algo a un niño que a través de un manipulativo físico o digital.
“Aprender el qué a través del cómo”.
Hola Smartick, gracias por enseñarnos.
Muy buena información, me ayudó bastante.
Gracias por desglosar de manera sencilla y básica los principios para la compresión y planteamiento de estas ecuaciones
me gustó
Gracias
muchas gracias me sirvió mucho para mi tarea de matemáticas
Se complica un poquito y con esto ya mejoré lo q no entendía. Ahora lo puedo compartir con todo mi salón para q lo entiendan y así tener un buen futuro sabiendo matemáticas gracias a la página Smartick
Una explicación clara y sencilla. Gracias!
Se me complicó un poquis pero sigo aprendiendo
Guau me ayudó de mucho porque aprendí muchas cosa
magnific!!
gracias
gracias, practicaré
Gracias César.
Lo practicaremos.