Las propiedades de los monomios
13 diciembre 2013
En este post vamos a ver qué son los monomios, cuáles son los componentes y qué propiedades tienen.
Índice
¿Qué es un monomio?
Un monomio es una combinación de números y letras relacionados por multiplicaciones (¡¡solo multiplicaciones!!) y los exponentes de las letras solo pueden ser números naturales.
Por ejemplo:
-5ax3
Es un monomio porque son combinaciones de números y letras relacionados solo por multiplicación y el exponente que aparece es un número natural.
-2m5 + m3
No es un monomio porque aparecen sumas y restas.
Ahora os propongo un ejercicio donde tenéis que decir si las siguientes expresiones algebraicas son monomios o no:
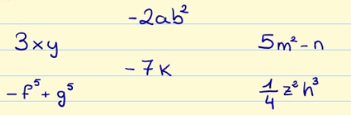
Partes de un monomio
A continuación detallamos los términos de los monomios.
Coeficiente
Es el número que multiplica a las letras.
Parte literal
Son las letras que aparezcan en el monomio con los exponentes.
Grado
Es la suma de los exponentes que tenga el monomio.
Variable
Son cada una de las letras que aparecen en el monomio.
Ejemplo de monomio
Vamos a ver las partes del siguiente monomio:
-2ab2
- Coeficiente: -2, es el número que acompaña a la parte literal
- Parte literal: ab2
- Grado: 1 + 2 = 3. El grado del monomio es 3
- Variable: a, b. Son las dos letras que aparecen en el monomio
¿Qué son dos monomios semejantes?
Dos monomios son semejantes cuando tienen exactamente la misma parte literal.
Por ejemplo, un monomio semejante al que hemos visto antes, -2ab2, sería cualquiera que tuviese la misma parte literal: ab2
-6ab2, 5ab2, 18ab2, ab2
Ahora os propongo que relacionéis los monomios de la columna de la izquierda con sus semejantes de la columna de la derecha.
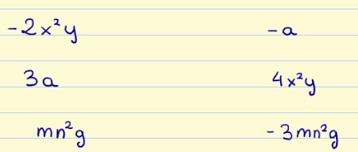
Vídeo tutorial de monomios
A continuación te mostramos un vídeo tutorial interactivo sobre monomios y polinomios, convertido en vídeo, que resuelven los alumnos de Smartick durante sus sesiones personalizadas.
Si quieres seguir aprendiendo matemáticas de primaria, adaptadas a tu nivel, no dudes en registrarte en Smartick y probarlo de manera gratuita.
Espero que te haya gustado nuestro post de hoy. ¡¡Hasta la semana que viene!!
25 Comentarios
Amo estas aplicaciones sobre las tareas para los niños
Me encantó esta aplicación de SMARTICK
Esta aplicación es muy buena
Hola, debe hacer la observación que los exponentes de las variables deben pertenecer a los números Naturales.
Hola Francisco:
Muchas gracias por tu comentario, hemos revisado el post y tienes razón, debe ser número natural en lugar de número no negativo.
Ya está corregido, gracias por ayudarnos a que el blog de Smartick no tenga errores 😉
¡Un saludo!
me gustaría entender más de las matemáticas, en realidad me cuesta mucho.
Hola, Jess:
Muchas gracias por tu comentario.
Si quieres aprender más contenidos como estos y así mejorar en matemáticas, basta con que te registres en Smartick. Tienes un periodo de prueba gratuito y sin ningún tipo de compromiso.
Si tienes alguna pregunta o duda adicional puedes escribir a mis compañeras del equipo pedagógico en [email protected]
¡Un saludo!
Gracias estaba en un examen y no sabía cómo hacerlo.
muchas gracias me ha servido de mucha ayuda ya que esto lo veo en este periodo académico y esta pagina me ha ayudado mucho en otras situaciones
me sirvió de mucho para mi tarea de matemática
muy bueno
me encantó muchas gracias, me enseñaste lo que vengo hace rato tratando de entender.
¡Muchas gracias por tu comentario, Miurel!
Es muy bueno me sirvió mucho
!Muy util y fácil para aprender y enseñar¡ Soy estudiante y buscaba sobre los monomios para mi tarea ahora lo entiendo muy bien.
!Gracias¡
más claro no puede ser
Me pareció muy bueno me sirvió de mucho gracias
Me parece extraordinariamente claro. ¡Soy abogado y lo entiendo ¡ Todavía me animo y estudio mates. Gracias Sara.
Me sirvió de mucha ayuda
Este método es muy bueno y me gusta
Le entendí muy bien me agrada mucho su programa
Muy buena estrategia de enseñanza
Felicidades
Felicitaciones, tu diseño y método para desarrollar el tema es espectacular, light y entendible.
Excelente didáctica de la enseñanza de expresiones algebraicas. Un buen aporte a los educadores .
Muchas gracias, Ana!
Un saludo!