Antes de ver algunos ejemplos de problemas de ecuaciones, vamos a repasar qué es una ecuación. Una ecuación es una igualdad en la que aparecen números y letras, que se llaman incógnitas, relacionados mediante operaciones matemáticas. Son una herramienta valiosa en matemáticas y en muchas áreas de la vida cotidiana. En el colegio nos enseñan algunas de las ecuaciones más importantes para la historia de la ciencia que se aplican en física y matemáticas.
Con frecuencia nos enfrentamos a situaciones que podemos representar escribiendo una ecuación. Los problemas de ecuaciones de primer grado sirven para representar situaciones en las que hay una cantidad desconocida que está relacionada con otras cantidades conocidas mediante una operación matemática. Al resolver una ecuación de primer grado se puede encontrar el valor de una cantidad desconocida.
Los problemas de ecuaciones se pueden ver como adivinanzas matemáticas. Te permiten resolver problemas y descubrir el valor de una cantidad desconocida.
Índice
¿Cómo resolver problemas de ecuaciones?
A continuación puedes ver los pasos que hay que seguir a la hora de resolver un problema de ecuaciones:
-
- Leer el problema despacio. Normalmente, la primera vez que leemos un problema nos quedamos con muy poca información, así que, es bueno leerlo varias veces.
- Escribir los datos que te da el problema y lo que te pregunta.
- Asignar una incógnita a lo que te están pidiendo.
- Escribir la ecuación que resuelve el problema. Hay que asegurarse de comprender lo que nos pregunta el problema.
- Resolver la ecuación. Recuerda que si la ecuación se puede simplificar, resolver la ecuación te resultará más fácil. Es muy importante saber resolver bien las ecuaciones de primer grado antes de pasar a resolver problemas de ecuaciones. Hay que dominar la resolución de ecuaciones reducibles.
- Comprobar la respuesta. No podemos olvidarnos de analizar si la solución que hemos encontrado tiene sentido y si responde a lo que nos han preguntado en el problema.
Ejemplos de problemas de ecuaciones en Smartick
En las sesiones de Smartick se trabajan varios tipos de problemas de ecuaciones de primer grado con una incógnita. A continuación vamos a ver un ejemplo de cada uno de los tipos.
Encontrar el valor de un número
En este ejemplo hay que encontrar el valor del número de objetos triangulares y el valor del número de objetos rectangulares que tiene Marina dentro de una caja.
Los datos del problema son:
- En la caja hay 20 objetos.
- El valor de los objetos rectangulares es cuatro veces el número de los objetos triangulares:
- Objetos triangulares → x
- Objetos rectangulares → 4x
- Nos piden: ¿Cuántos objetos hay de cada clase?
La ecuación de primer grado que resuelve este problema de ecuaciones es: 4x+x=20. El valor de x es 4. Por lo tanto, el número de cada tipo de objeto es 4 objetos triangulares y 16 objetos rectangulares.
Dividir un total en partes iguales
En este problema de ecuaciones hay que averiguar cuántas habitaciones hay en cada piso.
Los datos del problema son:
- En el hotel hay 57 habitaciones:
- Habitaciones del primer piso → x
- Habitaciones del segundo piso → 2x
- Nos piden: ¿Cuántas habitaciones hay en cada piso?
La ecuación de primer grado que resuelve este problema de ecuaciones es: x+2x=57. El valor de x es 19. Por lo tanto, en el primer piso hay 19 habitaciones y en el segundo piso hay 38 habitaciones.
Problemas de ecuaciones relacionados con edades
En este caso hay que encontrar el valor de la edad de Sara, Gema y Juan.
Los datos del problema son:
- Sara nació 4 años más tarde que su hermana Gema y un año antes que su hermano Juan:
- Edad de Sara → x
- Edad de Gema → x+4
- Edad de Juan → x-1
- Nos piden: ¿Cuántos años tiene cada uno?
La ecuación de primer grado que resuelve este problema de ecuaciones es: x+4+x+x-1=30. El valor de x es 9. Por lo tanto, Sara tiene 9 años, Gema 13 años y Juan 8 años.
Problemas de ecuaciones relacionados con precios
Hay que encontrar la cantidad de dinero que recibirá el hijo más pequeño.
Los datos del problema son:
- Sara ha recibido 1.200€.
- Decide repartirlo entre sus 4 hijos de esta forma:
- Primer hijo → x+30+30+30
- Segundo hijo → x+30+30
- Tercer hijo → x+30
- Cuarto hijo (el más pequeño) → x
- Nos piden: ¿Cuántos euros recibirá el hijo más pequeño?
La ecuación de primer grado que resuelve este problema de ecuaciones es: 1200=x+x+30+x+30+30+x+30+30+30. El valor de x es 255. Por lo tanto, el hijo más pequeño recibirá 255€.
Repartir una cantidad entre varias personas
Tenemos que encontrar el número de plazas que tenía el autobús en el que ha ido Beatriz con sus compañeros de clase de excursión.
Los datos del problema son:
- Si hubiesen ido todos los alumnos de la clase, cada uno hubiese pagado 5€.
- Han faltado 4 alumnos por lo que, cada uno, ha tenido que pagar 5,4€.
- Nos piden: ¿Cuántos plazas tenía el autobús?
- Número de plazas del autobús → x
La ecuación de primer grado que resuelve este problema de ecuaciones es: 5x=5,4(x-4). El valor de x es 54. Por lo tanto, el autobús tenía 54 plazas.
Contextos geométricos
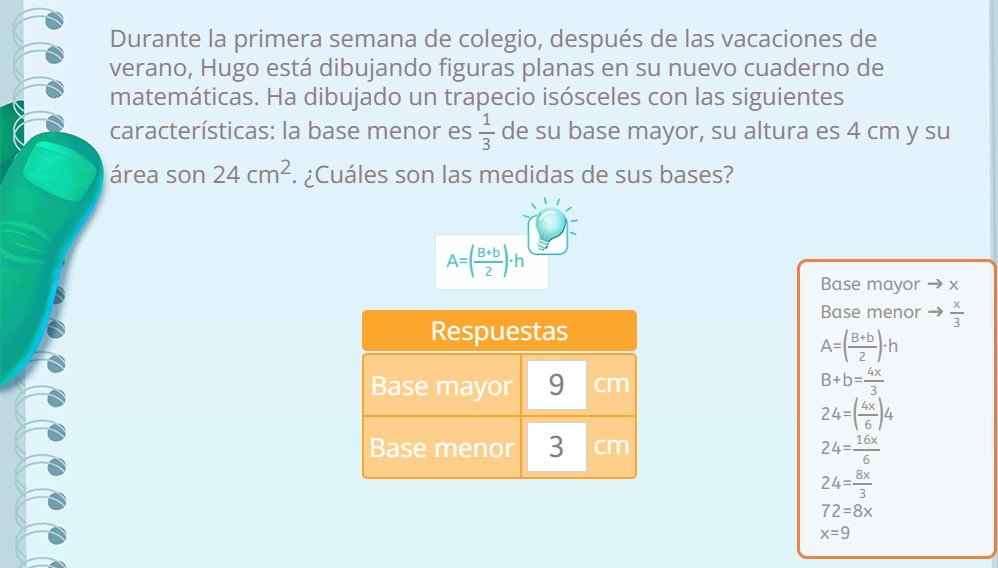
En este último problema de ecuaciones hay que encontrar las medidas de las bases del trapecio isósceles que ha dibujado Hugo en su cuaderno.
Los datos del problema son:
- Hugo ha dibujado un trapecio isósceles con las siguientes características:
- Medida de la base mayor → x
- Medida de la base menor → x/3
- Nos piden: ¿Cuáles son las dimensiones de cada una de las bases?
Para este problema hay que saberse la fórmula del área de un trapecio. La ecuación para resolver el problema de ecuaciones es 24=(4x/6)·4 . El valor de x es 9. Entonces, la base mayor mide 9 cm y la base menor 3 cm.
Es importante tomarse tiempo y practicar para mejorar en la resolución de problemas de ecuaciones. ¡Ánimo!
En Smartick puedes practicar y aprender a diario matemáticas de primaria, adaptadas a tu nivel, con sesiones de 15 minutos. Regístrate y pruébalo gratis. Después de hacer tu sesión diaria puedes ir al Mundo Virtual para competir con otros niños Smartick, personalizar tu avatar, practicar el entrenamiento cognitivo con más de 20 juegos y muchas cosas más que descubrirás al entrar.
Para seguir aprendiendo:
- Introducción a las ecuaciones: Cómo resolverlas fácilmente con ejemplos
- Barras de Singapur aplicadas a la resolución de ecuaciones algebraicas I
- Ecuaciones reducibles: ¿qué son? ¿cómo se resuelven?
- Balanzas en matemáticas: ¿Qué son y para qué se utilizan?
- Las ecuaciones más importantes para la historia de la ciencia
Es además monitora de ocio y tiempo libre.
Forma parte del equipo de didáctica de Smartick Matemáticas, le gusta transmitir conocimientos y valores a los demás y aprender.
Siente curiosidad por lo desconocido, le encanta pasar tiempo con sus seres queridos y viajar.
muy interesante