En la entrada de hoy vamos a ver la propiedad distributiva de la multiplicación respecto de la suma y de la resta.
La propiedad distributiva es una de las propiedades de la multiplicación que se aplica respecto a la suma o a la resta. Esta propiedad nos dice que si sumamos o restamos varios números y el resultado lo multiplicamos por otra cantidad, resulta igual a la suma o la resta de la multiplicación de cada uno de los términos por el número multiplicado, a(b + c) = ab + ac.
Vamos a ayudarnos de rectángulos y sus áreas para poder visualizarlo y así entender mejor la propiedad distributiva.
Propiedad distributiva de la multiplicación respecto de la suma.
En el siguiente ejemplo, a la izquierda de la igualdad, tenemos un rectángulo grande de base (b+c) y altura α formado por otros rectángulos más pequeños, uno azul y otro amarillo. La flecha hacia abajo nos indica el cálculo del área de ese rectángulo. A la derecha, hay un rectángulo azul de base b y altura α más otro de base c con la misma altura α. De nuevo, las flechas que caen de los rectángulos nos muestran las áreas de los dos rectángulos respectivamente.
Si os fijáis en las figuras es sencillo darse cuenta de que el área de los rectángulos no debería de variar entre los dos lados.
Esto nos muestra que da lo mismo calcular primero la suma que está dentro del paréntesis (la base del rectángulo grande de la izquierda) o aplicando la propiedad y distribuir el número, que está multiplicando, a ambos sumandos, y luego realizar la suma (calcular las áreas por separado y luego sumarlas). El resultado no varía.
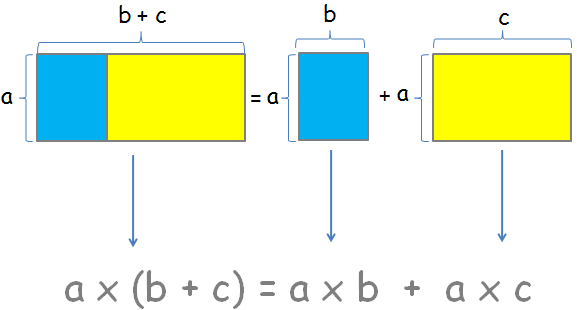
- Ejemplo 1
Pongamos un ejemplo con números:
5 x (10 + 2) = 5 x 10 + 5 x 2
Calculamos el lado izquierdo (calculamos el paréntesis primero): 5 x 12 = 60
Calculamos el lado derecho (se multiplica y luego se hace la suma): 50 + 10 = 60
Como veis, el resultado es el mismo, en ambos casos 60, independientemente de cómo lo hayáis calculado.
Propiedad distributiva de la multiplicación respecto de la resta.
Pasa lo mismo con la propiedad distributiva respecto de la resta. A continuación vemos que el rectángulo amarillo de la izquierda resulta ser el rectángulo grande de la derecha de base c menos el rectángulo azul de lado b.
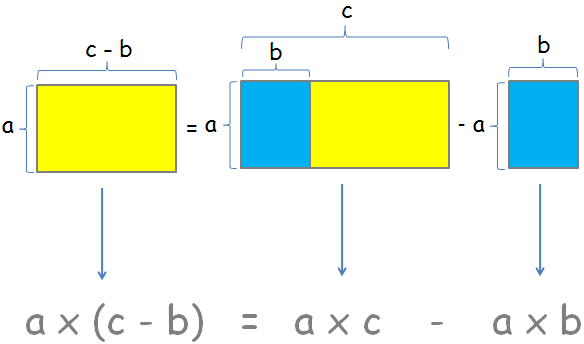
- Ejemplo 2
Os voy a poner un ejemplo con la resta también para que veáis lo fácil que es:
6 x (20 – 2) = 6 x 20 – 6 x 2
Calculamos el lado izquierdo: (primero hacemos la resta que está dentro del paréntesis) 6 x 18 = 108
Calculamos el lado derecho: (aquí se hacen primero las multiplicaciones) 120 – 12 = 108
¿Os habéis dado cuenta de que el resultado no varía? Genial, este es el resultado de aplicar la propiedad distributiva.
A la hora de usar esta propiedad, es importante aplicar el número que está multiplicando fuera del paréntesis a cada uno de los términos dentro del paréntesis.
¿Te ha sido útil este post? Date de alta en Smartick y aprenderás mucho más sobre la propiedad distributiva y otras propiedades de la multiplicación.
Para seguir aprendiendo:
- Propiedad distributiva desde el punto de vista geométrico
- Propiedad conmutativa de la multiplicación y de la suma
- Cómo realizar multiplicaciones con un modelo de área
- La propiedad distributiva de la multiplicación
- Propiedad asociativa en las multiplicaciones
- ¿Cómo se hacen divisiones de 3 cifras? II - 04/09/2017
- Potencias: paréntesis y signos negativos - 17/10/2016
- ¿Cómo se hacen divisiones de 3 cifras? - 19/09/2016








muy buena explicación
! Congratulation¡