En este post vamos a continuar desgranando el libro How I Wish I’d Taught Maths de Craig Barton sobre la educación basada en evidencias. Hoy vamos a destacar el papel que juegan los ejemplos en la enseñanza de las matemáticas y cómo utilizarlos en lugar de las meras definiciones y reglas instrumentales.
Ejemplos vs Definiciones
Es claro que los conceptos son la piedra angular de toda forma de conocimiento. El célebre filósofo prusiano Immanuel Kant afirmaba que la experiencia humana es ciega si no se cuenta con un sistema conceptual con el que aproximarse a ella. En matemáticas, donde (casi) todo es abstracto, se ha tendido a considerar que la mejor manera de presentar un concepto es mediante una definición verbal del mismo. Así, la enseñanza de algo nuevo partía de esas definiciones para dar paso después a los ejemplos y a la práctica.
Craig Barton nos presenta algunas definiciones matemáticas típicas, entre las que destaca la de ecuación. «Una ecuación es una proposición en la que dos expresiones matemáticas son iguales». Esta definición es correcta, pero presupone que sabemos de antemano lo que es una «proposición«, «expresiones matemáticas» y un sentido claro de cuándo son iguales y cuándo no.
Por ello, Barton nos propone recurrir mejor a los ejemplos para introducir el concepto.
Las siguientes expresiones sí que son ecuaciones:
- Y = X – 1
- Área = Base x Altura
- 2X + 1 = 0
En cambio, estas no lo son:
- X
- X + 1
- X = 3 – 2X = 1
En Smartick creemos en esta metodología levantada sobre evidencias. Por eso hemos desarrollado actividades como la siguiente, donde se trabaja la asimilación de los conceptos a partir de ejemplos elegidos.
Ejemplos vs Reglas
Algo parecido sucede también con las reglas instrumentales. Dentro del aula de matemáticas es habitual escuchar proclamas del tipo:
- «Dos menos seguidos son un más»
- «Para hacer la media, se suman todos y se divide entre el número de elementos»
- «Si está sumando, pasa restando»
Estas reglas pueden parecer beneficiosas en el corto plazo pues, evidentemente, pueden producir una sensación de mejora y saber hacer. Pero no implican en ningún caso una comprensión profunda de los conceptos. Además, en palabras de Skemp, el alumno que solo conoce reglas instrumentales fracasaría rotundamente si el profesor preguntara algo que no encajase a la perfección en aquellas.
De este modo, las corrientes didácticas actuales apuestan rotundamente por dirigir la atención hacia las ideas que se esconden detrás de las reglas. Se utilizan contextos interpretados que las dotan de sentido. Por ejemplo, en Smartick trabajamos las reglas habituales de la resolución de ecuaciones en el contexto de las balanzas.
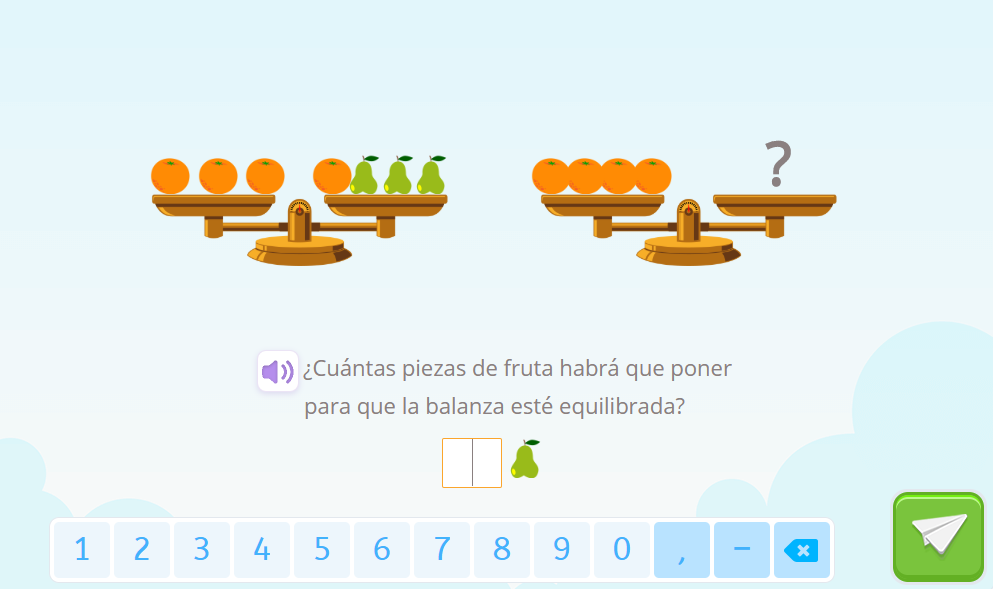
En la primera balanza, puede observarse que hay tres naranjas que pesan lo mismo que una naranja y tres peras. En lenguaje algebraico, representando por X a cada naranja y por Y a cada pera, la relación anterior se expresa como 3X = X + 3Y. La regla de la cancelación tiene ahora perfecto sentido y es que, si quitamos una naranja de cada plato, la balanza seguirá estando equilibrada.
Si quieres ir más allá de las reglas instrumentales y entender de verdad las matemáticas, únete a la comunidad Smartick. ¡Entra en Smartick y pruébalo gratis!
Referencias
- Barton, C. (2018). How I wish I’d taught maths. John Catt Educational Ltd
- Skemp, R.R. (1976) «Relational understanding and instrumental understanding», Mathematics Teaching 77 (1) pp 20-26
Para seguir aprendiendo:
- ¿Cuál es la diferencia entre serie y patrón?
- Expresiones algebraicas: ¿Qué son? ¿Para qué sirven?
- Educación basada en evidencias, la historia de Craig Barton
- ¿Cómo escribir sin faltas de ortografía?
- Suma con incógnita
Actualmente está cursando estudios de doctorado en Investigación en educación en la Universidad de Valladolid.
Es profesor de didáctica de la matemática en la Universidad de Valladolid y forma parte del equipo de desarrollo de contenidos de Smartick.
Entre sus aficiones destacan el tenis, el jazz y la escritura.
- Propiedades de las potencias - 13/04/2020
- El porqué de los criterios de divisibilidad - 02/03/2020
- Por qué son importantes los ejemplos en la enseñanza de las matemáticas - 27/01/2020