Hoy vamos a aprender a resolver actividades relacionadas con la representación de fracciones en la recta numérica y amplificación y simplificación de fracciones. Para ello necesitaremos utilizar fracciones equivalentes y recordar como ubicar números en la recta numérica.
Es fácil representar fracciones en la recta numérica cuando las divisiones de la unidad coinciden con el denominador de la fracción.
En este caso la recta numérica tiene una unidad con 3 divisiones. Y como el denominador de la fracción también es 3, coinciden. En este caso es sencillo saber que el marcador debe ir en la segunda posición de la recta numérica para representar la fracción 2/3.
Pero no es tan sencillo representar fracciones en la recta numérica cuando la unidad de la recta numérica no tiene el mismo número de divisiones que el denominador de la fracción.
Una estrategia es hacer coincidir estas dos cifras, las unidades de la recta numérica y el denominador de la fracción. Para ello debemos encontrar fracciones equivalentes en las que el denominador sí coincida con el número de divisiones de la unidad. Lo conseguimos amplificando o simplificando la fracción.
Índice
Fracciones amplificadas en recta numérica
Primero vamos a aprender cómo representar una fracción en una recta numérica cuando su unidad tiene más divisiones que el denominador de la fracción. En este caso no es tan obvia su representación.
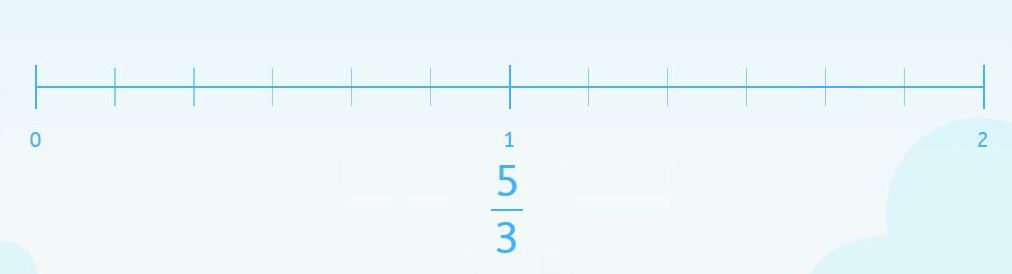
Por un lado, la recta numérica tiene dos unidades. Y cada unidad tiene 6 divisiones.
Y por otro, el denominador de la fracción es 3.
No coinciden y 6 es mayor que 3.
Podemos buscar una fracción equivalente, amplificando la que queremos representar, para obtener una fracción con denominador igual al número de divisiones de cada unidad de la recta numérica, seis.
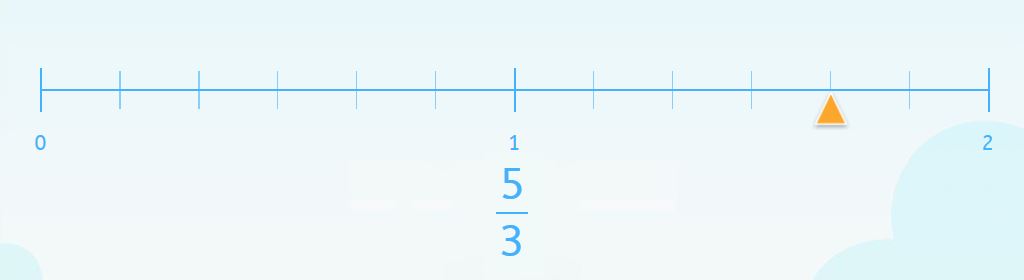
Ahora ya sabemos que el marcador debe ir en la décima posición de la recta numérica.
Fracciones simplificadas en recta numérica
Cuando la unidad de la recta numérica tiene menos divisiones que el denominador de la fracción, podemos utilizar otra estrategia similar para representarla.
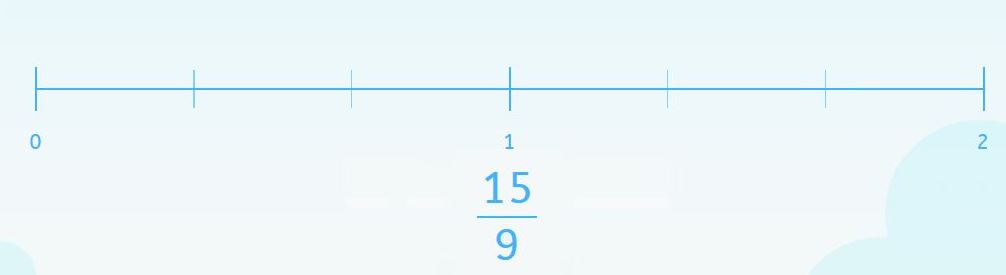
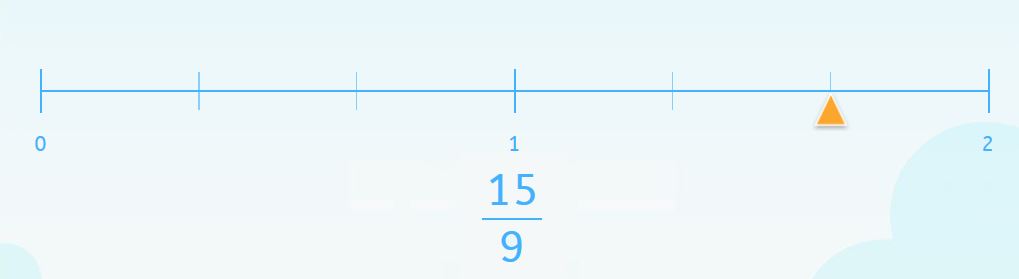
Aquí, cada unidad de la recta numérica tiene 3 divisiones y el denominador de la fracción es 9. Para hacer que coincidan podemos simplificar la fracción y obtener una fracción equivalente.
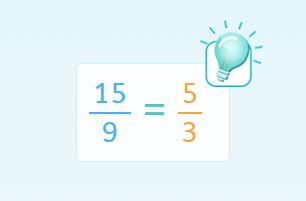
En este caso, el marcador estará situado en la quinta posición de la recta numérica.
Fracciones equivalentes en recta numérica que no comienza en cero
¿Y si añadimos un poco de complejidad a estas actividades? En cualquiera de los dos casos anteriores podemos pedir representar la fracción en una recta numérica en la que la unidad no tenga el mismo número de divisiones que el denominador de la fracción y que no empiece en cero.
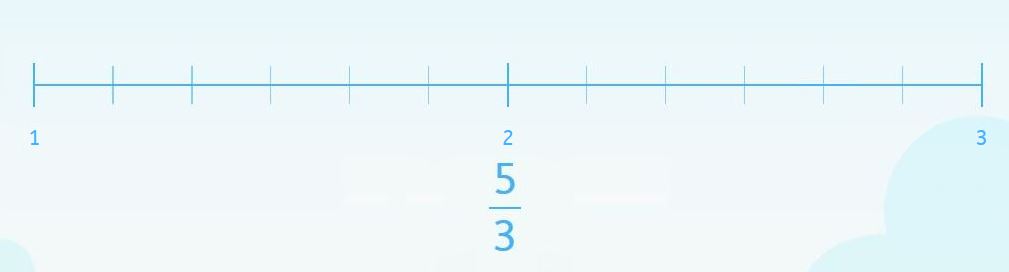
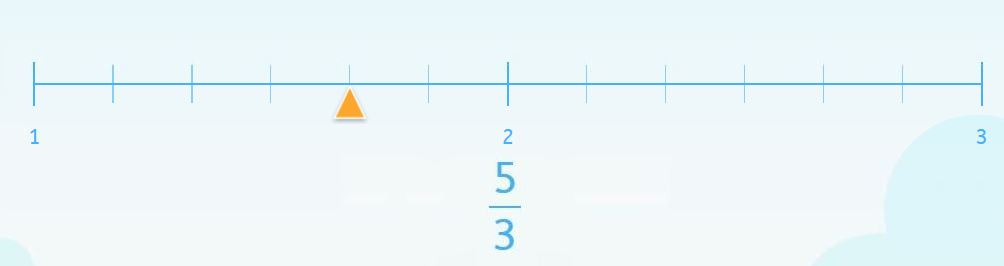
Este ejemplo es similar al primero, por lo que sabemos que tenemos que buscar una fracción equivalente por amplificación y que el marcador irá en la décima posición.
Pero la recta no comienza en uno, así que hay que imaginarse que antes existe una unidad que es desde la que se empieza a contar para colocar bien el marcador.
Y seguir contando a partir de ahí…
Si quieres practicar más sobre fracciones en la recta numérica, equivalentes, amplificación, simplificación y otros contenidos de matemáticas de infantil y primaria, adaptados a tu nivel, entra en Smartick, regístrate y pruébalo gratis.
Para seguir aprendiendo:
- Uso de la recta numérica para comparar fracciones
- Introducción a las fracciones
- Clasificación de fracciones: propias, impropias y unitarias
- Fracciones equivalentes: qué son y cómo calcularlas
- Ejercicios con fracciones equivalentes
Técnico Superior en Administración y Finanzas, Quiromasajista, Masajista Deportivo y Músico.
Forma parte del equipo de desarrollo de contenidos de Smartick.
Curioso por naturaleza, música y ciencia son dos de sus pasiones.
- Características de la práctica significativa - 23/03/2020
- Cómo representar fracciones en la recta numérica - 10/02/2020
- Diagramas de Venn en Smartick - 13/01/2020
Gracias, sí pude resolver el problema.
Muchas gracias por tu comentario, esperamos que te haya servido de ayuda nuestro post. 😊
Gracias por la explicación.
Hola, me sirvió bastante. Gracias maestro.
ESTE CONTENIDO ES MUY BUENO PARA MATEMÁTICAS
Me gusta aprender este tema tan interesante.