¿Alguna vez le has cambiado el tamaño a una fotografía y te has visto diferente? Más alto, con la cara más alargada, o menos… ¿O quizá has notado que, si en una carrera corres más rápido, tardas menos tiempo en llegar a la meta? En esas situaciones ya estás usando la proporcionalidad, aunque no lo sepas.
Ser proporcional significa que cuando una cantidad cambia, otra también lo hace, pero siguiendo una regla. A veces crecen juntas (como cuando aumentamos los ingredientes para hacer más tortitas) y otras veces una baja mientras la otra sube (como cuando pedaleamos más rápido y tardamos menos en recorrer el mismo camino).
En el post de hoy vamos a descubrir, paso a paso, qué significa ser proporcional y cómo entenderlo con ejemplos sencillos de la vida diaria.
Índice
¿Qué es una proporción?
Volviendo al ejemplo de cambiar el tamaño de una fotografía, si queremos cambiarle el tamaño pero que mantenga el mismo aspecto, debemos asegurarnos de que la razón entre la base y la altura de la fotografía se mantenga.
- La razón es una comparación entre dos magnitudes que se realiza mediante un cociente.
- Suele expresarse como una fracción o colocando dos puntos (:) entre las dos magnitudes.
Cuando hacemos una fotografía, esta tiene una base y una altura determinada.
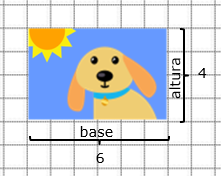
En este caso nuestra fotografía original tiene una base de 6 cm y una altura de 4 cm. La razón entre la base y la altura de la fotografía es de 6 : 4. Si dividimos 6 entre 4, obtenemos como resultado: 1,5. Esto quiere decir que la base de la fotografía es 1,5 veces más larga que su altura. O dicho de otro modo, significa que por cada cm de alto mide 1,5 cm de ancho.
Ahora que ya sabemos cuál es la razón entre la base y la altura de esta fotografía…
¿Cómo podemos calcular cuáles pueden ser sus nuevas medidas sin que se deforme?
Podemos hacerlo de dos maneras:
1. Encontrando una razón equivalente:
Multiplicando o dividiendo ambas magnitudes por el mismo número. Por ejemplo, podemos multiplicar la base y la altura por 2.
6 × 2 = 12 y 4 × 2 = 8
De esta manera la nueva base sería 12 y la nueva altura 8.
2. Encontrando la constante de proporcionalidad:
La constante de proporcionalidad es el resultado del cociente de las razones de una proporción. En nuestro ejemplo sería el resultado de dividir 6 entre 4.
6 : 4 = 1,5
Sabiendo esto, si queremos que la altura de nuestra fotografía sea 6, solo tenemos que multiplicar 6 por 1,5 para descubrir cuánto debe medir la base.
6 × 1,5 = 9
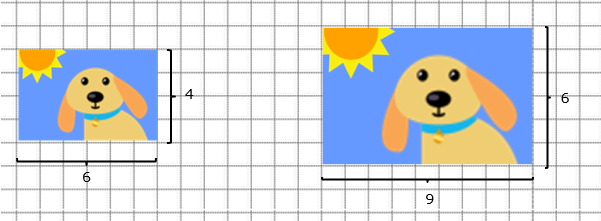
De cualquiera de las dos maneras hemos conseguido aumentar el tamaño de la fotografía sin modificar su relación de aspecto. ¡Esto ocurre porque hemos conservado la proporción!
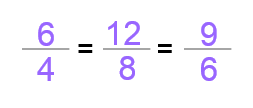
Cuando dos razones son iguales entre sí, decimos que forman una proporción. Una proporción es una igualdad de razones. La proporción es la correspondencia, el equilibrio o la simetría que existe entre los componentes de un todo.
Proporcionalidad
La proporcionalidad aparece cuando dos cantidades están relacionadas de manera que, cuando una cantidad cambia, la otra cambia de manera relacionada, manteniendo la proporción entre ellas.
En la vida diaria, la proporcionalidad y la proporción nos ayudan a entender situaciones como repartir objetos, calcular precios o medir ingredientes al cocinar.
Qué es la proporcionalidad
La proporcionalidad significa que dos magnitudes guardan una relación constante entre sí. Por ejemplo, si un tren recorre 100 kilómetros en 2 horas, en 4 horas recorrerá 200 kilómetros, manteniendo siempre la misma relación entre el tiempo y la distancia.
En la vida diaria, la proporcionalidad nos ayuda a calcular, comparar o repartir cosas de manera justa.
Cuando algo se hace proporcionalmente, quiere decir que se ajusta a ese equilibrio.
- Si duplicamos las cantidades de una receta, todos los ingredientes aumentan proporcionalmente.
- Si aumentamos el tamaño de un dibujo, todas las partes crecen en la misma medida, manteniendo la forma original.
En otras palabras, hacer algo proporcionalmente es mantener la misma relación, aunque las cantidades cambien.
Proporcionalidad directa
La proporcionalidad directa ocurre cuando dos cantidades son directamente proporcionales, es decir, si una aumenta, la otra también aumenta en la misma proporción. Mantienen siempre la misma relación proporcional. En otro post de Smartick se explica de forma más detallada qué es la proporcionalidad directa y para qué sirve, te animo a que lo visites.
Ejemplos:
-
Si compras 1 chocolatina, pagas 1 €.
-
Si compras 2 chocolatinas, pagas 2 €.
-
Si compras 5 chocolatinas, pagas 5 €.
Otro ejemplo:
-
Si un coche recorre 50 km en 1 hora, en 2 horas recorrerá 100 km, y en 3 horas 150 km. La distancia recorrida es directamente proporcional al tiempo de viaje.
Proporcionalidad inversa
La proporcionalidad inversa ocurre cuando dos cantidades son inversamente proporcionales, es decir, si una aumenta, la otra disminuye. Aquí la relación proporcional se mantiene, pero de manera inversa: más de una cosa significa menos de la otra. Para comprenderlo mejor y ver más ejemplos prácticos, puedes profundizar en nuestro post sobre proporcionalidad inversa.
Ejemplos:
-
Si 2 amigos limpian una habitación, se tarda 3 horas.
-
Si 3 amigos ayudan, se tarda menos tiempo, 2 horas.
-
Si 6 amigos ayudan, se tarda aún menos, 1 hora.
Otro ejemplo:
-
Si un coche va más rápido, tarda menos tiempo en llegar a su destino.
-
60 km/h → 2 horas
-
120 km/h → 1 hora
-
En la proporcionalidad inversa, siempre se respeta la relación entre las cantidades, pero al aumentar una, la otra disminuye.
Problema de proporcionalidad
La mejor manera de trabajar y entender la proporción es mediante la práctica. ¡Vamos a verlo con un problema!
«El mes pasado fue el cumpleaños de Lola e hizo una tarta para sus 16 amigos siguiendo la receta que le dio su abuela. Mañana es el cumpleaños de su hermano y quiere hacer una tarta para celebrarlo. Ha comprado todos los ingredientes, pero no sabe qué cantidades debe utilizar para hacer una tarta para 4 personas.»
Pero como tiene la receta de la tarta para 16 personas va a intentar sacar las proporciones de los ingredientes para hacerla. Vamos a ver cómo lo hace…
La receta es para 16 personas, que son 4 veces más personas que las que van a comer la tarta que quiere hacer ahora Lola. Por lo tanto las cantidades de cada ingrediente serán 4 veces menos que las cantidades que necesitó para hacerla para 16 personas.
Por ejemplo, si para 16 personas se necesitan 8 huevos, para 4 personas se necesitaran menos huevos, pero debemos mantener la misma proporción. Y para ello Lola divide cada cantidad de cada ingrediente entre 4.
Para no equivocarse decide hacer una tabla.
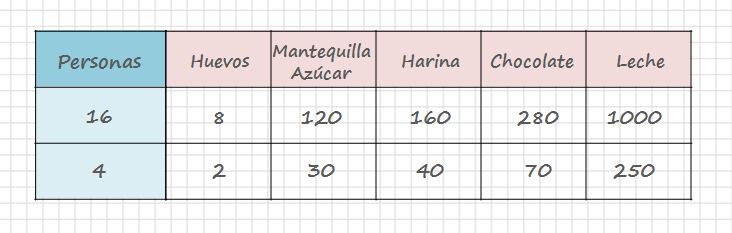
Estas son las operaciones que ha hecho Lola para mantener la misma proporción:
- 8 huevos entre 4: 8 ÷ 4 = 2 huevos
- 120 gramos de azúcar y de mantequilla: 120 ÷ 4 = 30 gramos
- 160 gramos de harina: 160 ÷ 4 = 40 gramos
- 280 gramos de chocolate: 280 ÷ 4 = 70 gramos
- 1000 mililitros de leche: 1000 ÷ 4 = 250 mililitros
Ahora ya sabéis qué cantidad de ingredientes debemos utilizar para hacer una tarta para 4 personas, y podéis seguir los mismos pasos para hacer una para la cantidad de personas que queráis, ¡siempre que mantengáis la proporción!
Si queréis seguir aprendiendo y practicando actividades de proporción podéis entrar en estos enlaces:
En resumen, entender la proporcionalidad ayuda a los niños a razonar de manera lógica y a resolver problemas de la vida diaria, desde repartir objetos hasta calcular precios o tiempos.
Es importante que los padres acompañen este aprendizaje con ejercicios prácticos, guiando a los niños y reforzando su comprensión de las relaciones proporcionales. Además, en Smartick, los niños pueden practicar de forma personalizada y adaptada a su nivel, de manera divertida y progresiva, fortaleciendo sus habilidades matemáticas día a día. Regístrate ahora en Smartick y pruébalo gratis.
Para seguir aprendiendo:
- Relación de proporcionalidad con un problema
- Proporcionalidad inversa. ¿Qué es?
- Ejercicios de números proporcionales
- Problemas con regla de tres simple
- Proporcionalidad inversa, regla de tres inversa
Mi profesión es totalmente vocacional, he trabajado en escuelas de educación libre en Madrid y fuera de España en proyectos de educación en India y Nicaragua.
Mi pasión son los niños y viajar a países de culturas muy diferentes.
- Barras de Singapur aplicadas al concepto de porcentaje - 07/08/2017
- Geometría y figuras planas con la ayuda del Tangram - 10/07/2017
- Qué es una división. Conceptos basicos - 12/06/2017
Tiene una pinta fantástica, tomamos nota para hacerla el próximo fin de semana. Saludos cordiales.
bien