En el post de hoy vamos a aprender sobre dos términos que suenan un poco raros y en ocasiones se confunden, pero que los podemos encontrar en todas partes: cóncavo y convexo. Puede que no los hayas escuchado antes, o puede que sí y que incluso te los hayan explicado de otra forma, pero hoy veremos sus diferencias y lo fácil que es confundir ambos términos. Además veremos ejemplos prácticos y divertidos que harán que nunca olvides qué son cóncavo y convexo.
¡Vamos a descubrir qué significan! Seguro que al terminar de leer este post serás capaz de reconocerlos siempre. 😉
Índice
Diferencia entre cóncavo y convexo
Para ver las diferencias entre cóncavo y convexo, primero debemos saber que hay diferentes situaciones en las que encontramos las palabras cóncavo y convexo.
- En nuestro entorno cotidiano podemos utilizar cóncavo para hablar de superficies o formas que se hunden o están hacia adentro, por ejemplo cuando miramos el interior de un cuenco desde arriba. Mientras que hablamos de convexo cuando la superficie o la forma está redondeada o hacia afuera.
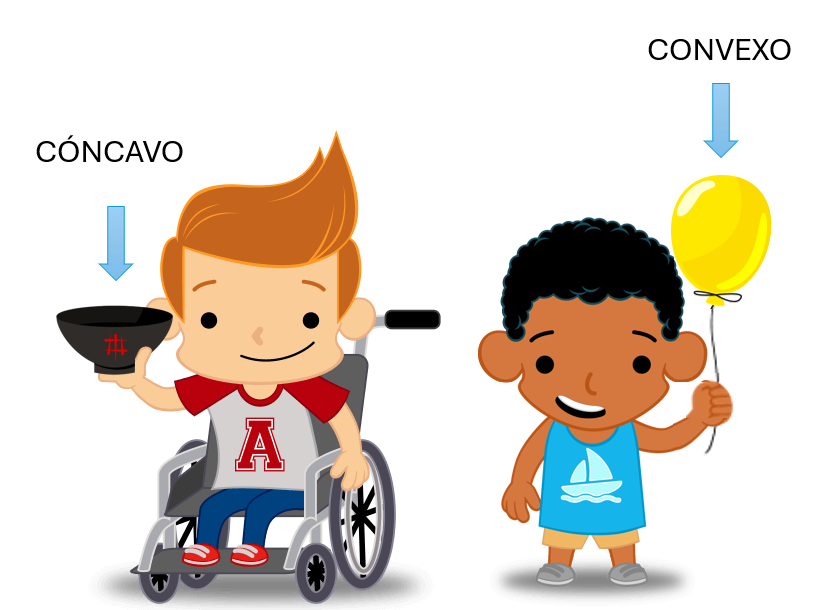
Es muy importante tener en cuenta que los objetos no son cóncavos y convexos, sino que dependiendo de cómo los miremos, desde arriba o desde abajo, podremos decir cómo son. Porque, fijaos en el cuenco que tiene Leo en la mano, si le damos la vuelta, en lugar de tener una superficie cóncava que se hunde, tendríamos una superficie convexa al redondearse.
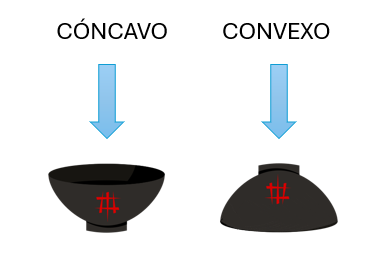
- En matemáticas es habitual encontrar las palabras cóncavo y convexo ya que son una de las características de las formas con relleno como los polígonos y en las curvas de las funciones.
- En espejos y lentes:
- Un espejo cóncavo tiene una superficie hundida y se utiliza para concentrar la luz o hacer que las imágenes se vean más grandes.
- Un espejo convexo por otro lado, tiene una superficie curvada hacia el exterior lo que provoca que la visión se expanda.
- En las lentes se utiliza especialmente en las gafas. Cuando la lente es cóncava, es más delgada por el centro que por los bordes y se utiliza para corregir la miopía, haciendo que los objetos que están lejos se vean más nítidos.
- Mientras que si la lente es convexa, es más gruesa en el centro y se usa para corregir la hipermetropía, haciendo que los objetos cercanos se vean más nítidos.
- En la naturaleza, podemos encontrar formas cóncavas como los valles, los lagos o incluso los cráteres de la luna. Y formas convexas como las cumbres de las montañas, las colinas o incluso el caparazón de una tortuga.
Cóncava
Convexa
Concavidad
Como hemos visto concavidad hace referencia a la cualidad de ser cóncavo. Las superficies, figuras o curvas que tienen una forma hundida o hacia adentro, como si fueran un cuenco visto desde arriba.
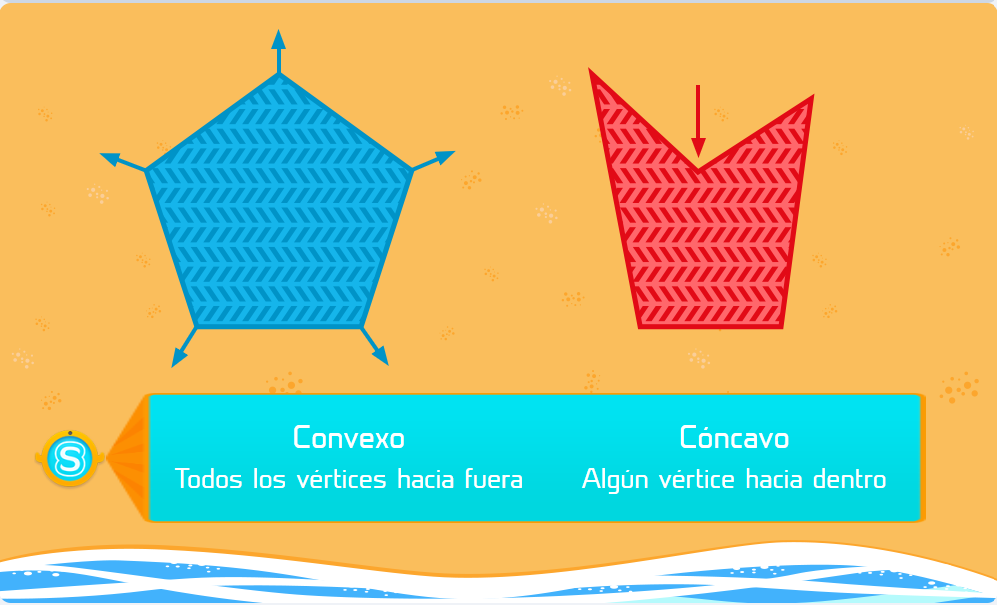
- Superficies o figuras cóncavas. Una superficie es cóncava cuando al trazar una línea entre dos puntos de esa superficie, la línea puede salir de la figura, porque la forma está hundida o curvada hacia dentro.
- Curva cóncava. En el caso de las funciones y especialmente para llegar a un acuerdo matemático en cuanto a cómo nombrarlas se decidió que las funciones con curvatura positiva se llamarían curvas cóncavas al tomar como referencia mirarlas desde la parte superior de la imagen.
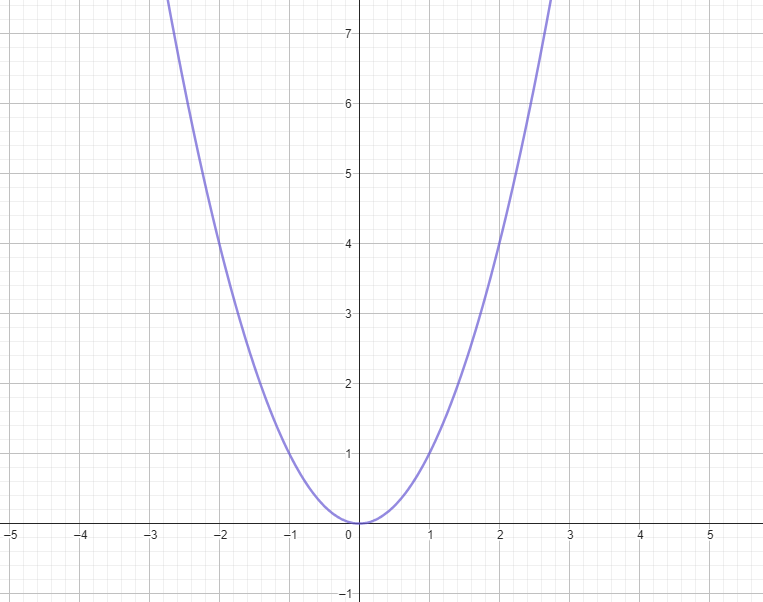
Convexidad
La convexidad, por tanto, hace referencia a la cualidad de ser convexo. Las superficies, curvas o figuras que tienen una forma que sobresale o se abulta hacia afuera.
- Superficies o figuras convexas. Una superficie es convexa si, al trazar una línea entre dos puntos cualesquiera de esa superficie, la línea siempre queda dentro de la figura. Esto se ve claramente en los círculos, pero también ocurre por ejemplo con polígonos regulares, los que tienen todos sus lados y ángulos iguales.
- Curva convexa. Del mismo modo que en la curva cóncava, se llegó al acuerdo de hablar de curvatura negativa cuando la función formaba una curva convexa al mirarla desde la parte superior de la imagen.
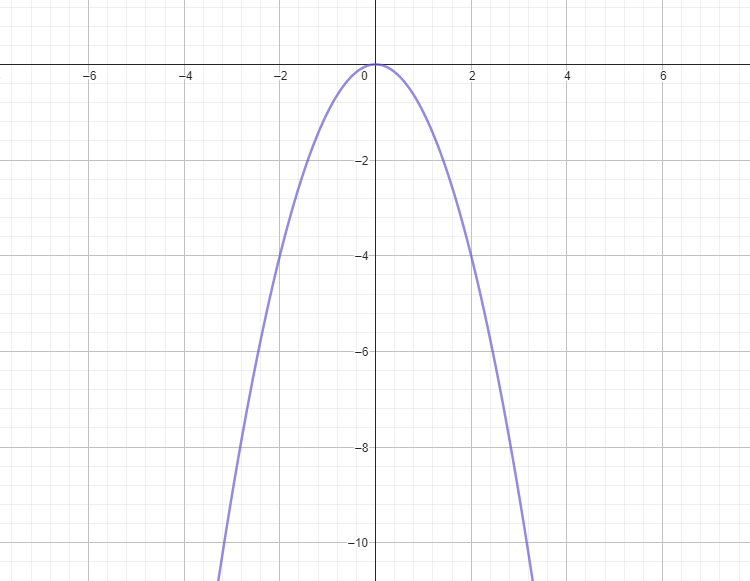
Punto de inflexión
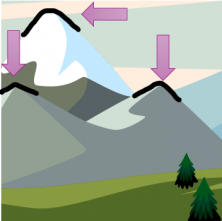
Pero, ¿qué ocurre cuando cóncavo y convexo se suceden? Imaginemos que estamos atravesando varias colinas. Si subimos por un lado de la primera, esta forma será convexa, al llegar a la cima sigue siendo convexa y cuando empezamos a bajarla también es convexa. Pero, hay un momento en el que estamos bajando y la forma empieza a ser cóncava. Ese punto en el que deja de ser convexo y empieza a ser cóncavo es el llamado punto de inflexión.
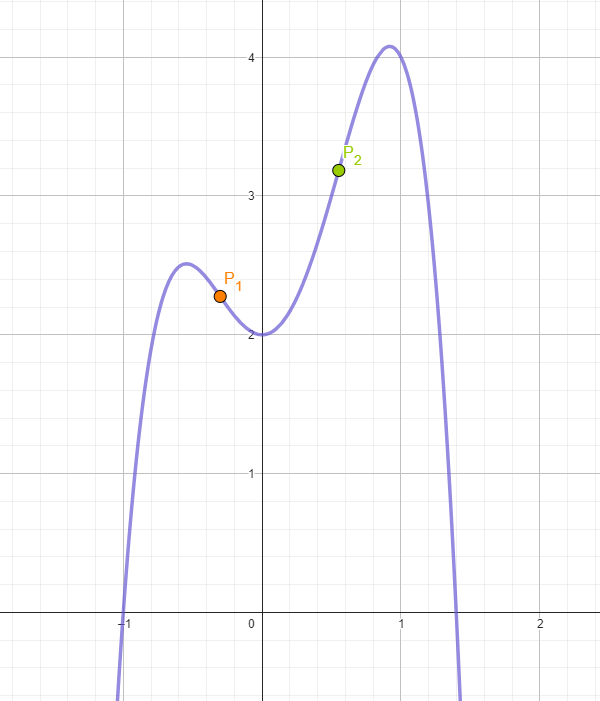
El punto de inflexión es el lugar donde una forma deja de ser cóncava o convexa y pasa a ser lo contrario. En la función que tienes a continuación encontrarás dos puntos de inflexión.
- En el primer punto P₁, el naranja, vemos como pasamos de una curva convexa a una cóncava.
- En el segundo punto P₂, el verde, vemos como la curva cóncava se convierte en una curva convexa.
Actividades para practicar
Hay muchos objetos que se pueden clasificar en cóncavo y convexo. Puedes buscar por casa algunos o dibujar tus propios objetos cóncavos y convexos. Pero te voy a proponer un experimento. Busca una cuchara de metal y fíjate en qué ocurre si te ves en la parte cóncava o si te ves en la parte convexa. ¡Es muy divertido!
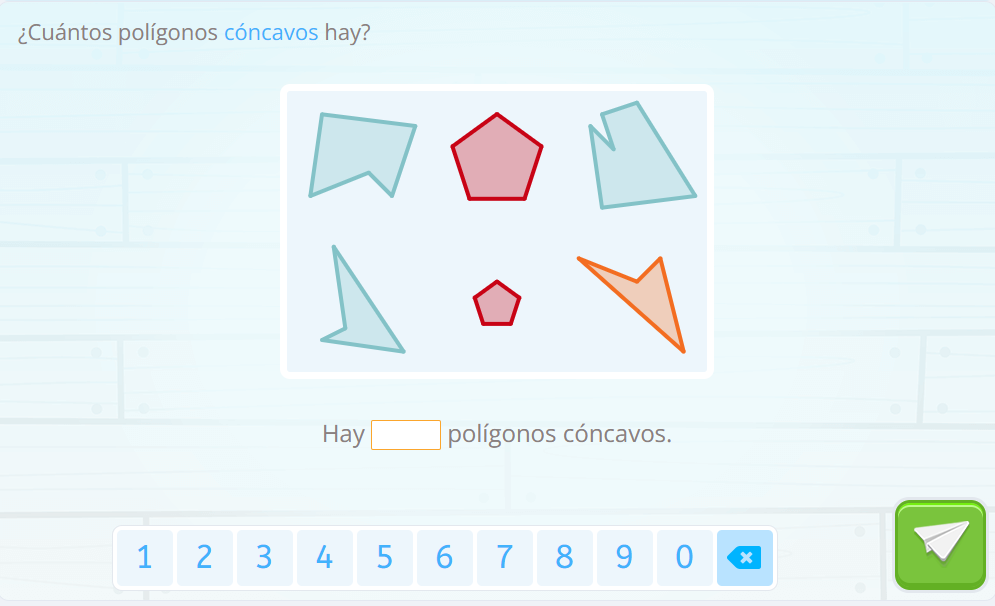
Ahora que ya has visto varios ejemplos, ¿podrías resolver estas actividades que aparecen en las sesiones de Smartick?
Como has podido descubrir hay muchos objetos cóncavos y convexos que encontramos fácilmente en nuestro día a día. Si quieres seguir aprendiendo sobre ello puedes acceder al siguiente enlace:
Si te ha gustado este post sobre cóncavo y convexo y quieres seguir practicando y desarrollando tus habilidades, regístrate en Smartick. Aprovecha y disfruta de nuestro método online de aprendizaje personalizado para niños de 4 a 14 años, que se adapta a tu propio ritmo de aprendizaje.
Para seguir aprendiendo:
- ¿Qué son las figuras geométricas sólidas o cuerpos geométricos?
- Trapezoide. Definición, tipos y ejercicios
- Curvas abiertas y cerradas
- Líneas abiertas. Geometría de primaria
- Figuras geométricas: El círculo
Forma parte del equipo de Didáctica de Smartick y le encanta contribuir a que los niños y niñas aprendan divirtiéndose.
Siempre que puede le gusta viajar y conocer lugares nuevos y en su tiempo libre le apasionan los juegos de mesa.