En el post de hoy vamos a hablar de un tema que ya habíamos trabajado con anterioridad en Smartick, los cuerpos geométricos, pero esta vez vamos a enseñaros a calcular su área.
En post anteriores hemos trabajado las áreas de las figuras planas y los tipos de cuerpos geométricos, así que hoy unificaremos estos dos contenidos viendo cómo se calcula el área de los cuerpos geométricos.
Índice
El área de los cuerpos geométricos
Cuando nos referimos al área estamos hablando del cálculo de la superficie que ocupa algo, en este caso un cuerpo geométrico. Para acordarnos fácilmente de qué es, nos podemos imaginar que es como pintar todas las caras de ese cuerpo geométrico. Por ejemplo, tenemos un dado gigante y queremos pintarlo entero de un color, tendríamos que calcular su superficie para saber cuánta pintura necesitaremos para cubrir sus seis caras.
Recuerda que la unidad de medida más común para hallar la superficie son los metros cuadrados (m²), pero te pueden preguntar por centímetros cuadrados si estás hallando la superficie de algo más pequeño como la superficie de una mesilla, o kilómetros cuadrados, cuando tienes que calcular la superficie de un terreno extenso.
Para calcular el área de los cuerpos geométricos tendremos que conocer las medidas de sus distintos lados. Como los cuerpos geométricos están compuestos por varias caras y estas pueden ser triangulares, rectangulares, pentagonales… para hallar el área del cuerpo geométrico, tendremos que hallar el área de cada una de sus caras y sumarlas todas.
Un consejo que puede ayudaros bastante a hallar las áreas de cualquier cuerpo geométrico es descomponerlo y ver las figuras planas que lo componen.
Veamos algunos ejemplos.
Los cuerpos geométricos y sus áreas
- Poliedros regulares
Son también conocidos como sólidos platónicos y se caracterizan por tener todas sus caras iguales. Son cinco: tetraedro, cubo o hexaedro, octaedro, dodecaedro e icosaedro.
Por tanto, para hallar su área deberemos calcular la superficie de una de sus caras y multiplicarla por el número de caras que tenga el poliedro regular. Veamos el ejemplo con este cubo que tiene 5 cm de lado: 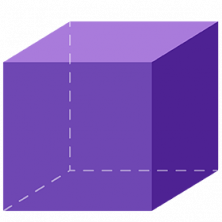
Empezaremos calculando el área de una de sus caras y como sabemos que su lado mide 5 cm, calculamos el área 5 × 5 = 25 cm².
Ya sabemos que una de sus caras tiene 25 cm². Como tiene 6 caras, multiplicamos 25 × 6 = 150 cm²
La superficie de este cubo es de 150 cm²
- Prismas
Los prismas son cuerpos geométricos con dos bases paralelas, que pueden ser cualquier figura plana, pero siempre las mismas, y que sus caras laterales son paralelogramos.
Por tanto, para hallar el área total de los prismas tendremos que hallar el área lateral y sumarle el área de las bases.
Ejemplo de prismas de base pentagonal visto de pie, tumbado y cómo quedaría descompuesto:



Viendo este prisma observamos que sus bases son dos pentágonos regulares. Por tanto, empezaremos hallando el área de esos 2 pentágonos. Luego, hallaremos el área lateral, que es la suma del área de los 5 rectángulos laterales.
Por último, para hallar el área total, sumaremos el área lateral y el área de las bases.
- Pirámides
Las pirámides son cuerpos geométricos con una base poligonal en la que todas sus caras laterales son triángulos que se encuentran en un punto común llamado vértice.
Por tanto, para hallar el área total de las pirámides tendremos que hallar el área lateral y sumarle el área de la base.
Ejemplo de pirámide de base cuadrada vista de pie y tumbada:


Ejemplo de pirámide de base cuadrada descompuesta:

Podemos ver que su base es un cuadrado, así que calcularemos primero su área. Luego, hallaremos el área lateral, que es la suma del área de los 4 triángulos laterales.
Por último, para hallar el área total, sumaremos el área lateral y el área de la base.
- Cilindros
Un cilindro es uno de los cuerpos geométricos redondos. El cilindro tiene dos bases circulares paralelas y un rectángulo formado con la longitud de la circunferencia y la altura del cilindro.
Por tanto, para hallar el área total de los cilindros tendremos que hallar el área lateral y sumarle el área de las bases circulares.
Ejemplo de cilindro:
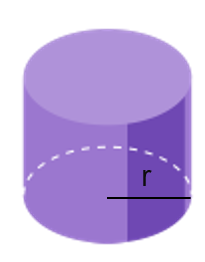
Empezaremos por hallar el área de las bases para ello calcularemos el área de una circunferencia y como hay dos lo multiplicaremos por 2. Por tanto, haremos 2 × (π × radio²).
Ahora toca calcular el área lateral, recordemos que el área del rectángulo es base × altura, en este caso la base del rectángulo es la longitud de la circunferencia. Por tanto, utilizamos la fórmula de la longitud de la circunferencia que es 2 × π × radio y lo multiplicamos por la altura del cilindro.
Por último, para hallar el área total, sumaremos el área lateral y el área de las bases.
- Conos
Los conos son cuerpos geométricos redondos porque, al igual que los cilindros, cuentan con una base circular que les permite rodar por el espacio. Se forman con base circular y una base lateral que se curva desde la base hasta un vértice único.
Para hallar su área total tendremos que hallar el área lateral y sumarle el área de la base circular.
Ejemplo de cono:
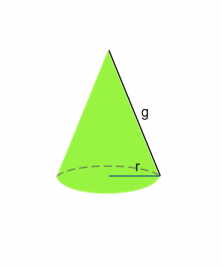
El área de la base, al igual que con el cilindro, calcularemos el área de una circunferencia con la fórmula: π × radio². Pero para que calculemos el área lateral necesitaremos conocer la generatriz (g), con ella aplicamos la fórmula π × radio × g y conseguiríamos el área lateral.
La generatriz la podemos sacar del triángulo rectángulo formado por la altura y el radio de la base, siendo la hipotenusa la generatriz.
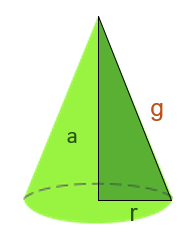
Por último, sumamos el área lateral y el área de la base y conseguimos el área total.
- Esferas
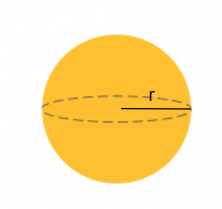
Terminaremos el post hablando del último de los cuerpos geométricos redondos, las esferas. Estas son cuerpos de revolución formadas por el conjunto de todos los puntos del espacio que equidistan de un punto llamado centro.
Para hallar su área total tendremos que recurrir directamente a la fórmula que es 4 × radio².
Ejemplo de esfera:
Enlaces de interés
Si quieres repasar más sobre estos temas aquí tienes unos enlaces de interés:
- ¿Qué es un prisma?
- Curiosidades sobre las figuras geométricas
- Cómo construir un icosaedro con gominolas
Para seguir desarrollando tus habilidades geométricas y aprender matemáticas y comprensión lectora, regístrate en Smartick. Aprovecha y disfruta de nuestro método online de aprendizaje personalizado para niños de 4 a 14 años, que se adapta a tu propio ritmo de aprendizaje.
Para seguir aprendiendo:
- Cilindro: características, ejemplos y cómo calcular área y volumen
- ¿Qué son las figuras geométricas sólidas o cuerpos geométricos?
- ¿Qué es un prisma? Descúbrelo con ejercicios resueltos
- Geometría: Prismas
- Perímetro: qué es y cómo calcularlo en cada figura







