Acostumbrados a trabajar con figuras geométricas en nuestros cuadernos, libros de texto o la pantalla de nuestra tableta, hoy vamos salir de lo cotidiano y a descubrir los misterios que esconden algunas figuras geométricas y cómo el ser humano se ha enfrentado o aprovechado de ellos.
En este post hablaremos de dos figuras geométricas: el pentágono regular y el triángulo.
Pentágono regular
Empezamos por el pentágono regular y un viejo conocido, Pitágoras, que fue un matemático y filósofo de la Antigua Grecia. Seguramente conozcas su famoso teorema sobre los triángulos rectángulos: El Teorema de Pitágoras.
Hizo muchas y grandes aportaciones al mundo filosófico y matemático y las compartió con unos pocos en su escuela. Digo unos pocos porque se trataba de una escuela un tanto elitista a la que no todos podían acudir. Los miembros de la Escuela Pitagórica se identificaban unos a otros mediante el pentágono estrellado, que surge de unir los vértices no consecutivos de un pentágono regular.
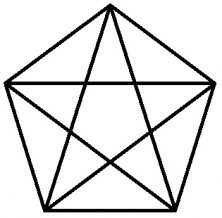
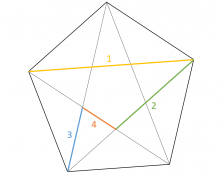
Su filosofía se apoyaba en la creencia de que los números son el principio de todas las cosas y que todos los elementos del mundo se relacionaba mediante un orden numérico de números fraccionarios. Pero cuando descubrieron que su “símbolo secreto” no respetaba esto, Pitágoras hizo jurar a los miembros de su escuela el silencio sobre este hallazgo. En esta figura geométrica aparecen cuatro segmentos de diferentes longitudes. Las divisiones del primero entre el segundo, del segundo entre el tercero y del tercero entre el cuarto, dan todas el mismo número, un número muy particular e irracional (como el número π), el número aureo o número de oro, representado con la letra φ.
Triángulo
En relación a la segunda figura geométrica de la que hablaremos en el post de hoy, el triángulo, encontramos una anécdota curiosa que tiene como protagonista a Thales de Mileto, otro matemático de la antigüedad que enunció 5 teoremas muy importantes para la geometría proyectiva.
El primero de estos teoremas determina que «si en un triángulo se traza una línea paralela a cualquiera de sus lados, se obtiene un triángulo que es semejante al triángulo dado». Así se consiguió calcular la altura de la inexplorable pirámide de Keops construida por los antiguos egipcios. A partir de esta premisa se puede establecer la relación de proporcionalidad que existe entre los lados de dos triángulos semejantes, lo cual fue la clave de los cálculos de Thales.
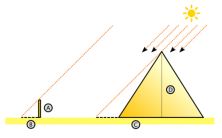
Thales clavó un palo en el suelo de forma perpendicular y, sabiendo la longitud del mismo, midió su sombra. Calculó el cociente entre ambas medidas y luego midió la sombra de la pirámide de Keops y añadió la distancia hasta el centro de la misma. Sabía que el cociente entre esta distancia y la altura de la pirámide debía ser la misma que el obtenido entre el palo y su sombra.
Donde él ya conocía A, B y C.
¿Te atreves a hacerlo tú mismo? Busca un edificio de tu barrio o un árbol de un parque cercano y calcula su altura. Te darás cuenta de lo útil que puede ser la geometría, elevándonos a lo más alto de las más altas torres sin movernos del suelo.
Y si quieres saber algo más sobre los secretos que esconden las figuras geométricas te planteo algunas preguntas que han entretenido a muchos matemáticos a lo largo de la historia:
- ¿Por qué los panales de las abejas tienen forma de hexágono regular?
- ¿Cuál es la figura geométrica que, con menos perímetro, delimita más superficie?
- ¿Cómo dibujar triángulos rectángulos sin el uso de regla, escuadra, cartabón o cualquier herramienta que me permita copiar un ángulo recto?
Para seguir aprendiendo:
- Geometría y figuras planas con la ayuda del Tangram
- Figuras geométricas: el triángulo
- Figuras geométricas. Clasificación, tipos y ejemplos
- Polígonos regulares e irregulares: Descubre los tipos de polígonos
- Perímetro: qué es y cómo calcularlo en cada figura
Forma parte del equipo de desarrollo de contenidos de Smartick, donde se encarga de elaborar secuencias didácticas, ejercicios y tutoriales. También colabora en la atención de sugerencias de los alumnos en "El Pozo".
Cree en la educación como motor de desarrollo de la sociedad y en el conocimiento como clave esencial para el crecimiento individual.
Sus pasiones son la educación en todas sus modalidades, montar en bici, el senderismo y escaparse de acampada siempre que puede.
- Number talks: Aprende matemáticas hablando - 31/05/2023
- Estrategias de cálculo mental para niños - 25/03/2021
- Ecuaciones reducibles: ¿qué son? ¿cómo se resuelven? - 03/02/2020
Qué valiosa información, espero que se vaya actualizando, gracias por tan buen trabajo.
Me interesa esta página