En este post vamos a ver qué es el teorema de Pitágoras y alguna de sus demostraciones. Por último, veremos cómo resolver un problema aplicando este teorema.
Índice
¿Qué es el teorema de Pitágoras?
Un teorema en matemáticas es una proposición o afirmación que se puede demostrar de manera lógica y rigurosa, utilizando reglas y principios matemáticos. Un teorema es siempre válido y se utiliza para establecer verdades fundamentales en el ámbito matemático.
El teorema de Pitágoras tiene este nombre porque su demostración, sobre todo, es esfuerzo de la escuela Pitagórica. El pitagorismo fue una corriente filosófica y matemática asociada al pensador griego Pitágoras, quien vivió en el siglo VI a.C. Aunque es difícil separar los aspectos históricos reales de las leyendas que rodean a Pitágoras, se le atribuye la fundación de la escuela Pitagórica donde a pesar de la época, podían estudiar tanto hombres como mujeres, y se aprendía matemáticas por la satisfacción de plantear y resolver problemas matemáticos en una época donde solo los arquitectos y los ingenieros eran obligados a estudiarlas.
El teorema de Pitágoras dice que, en un triángulo rectángulo, el área del cuadrado construido sobre la hipotenusa es igual a la suma de las áreas de los cuadrados construidos sobre los catetos.
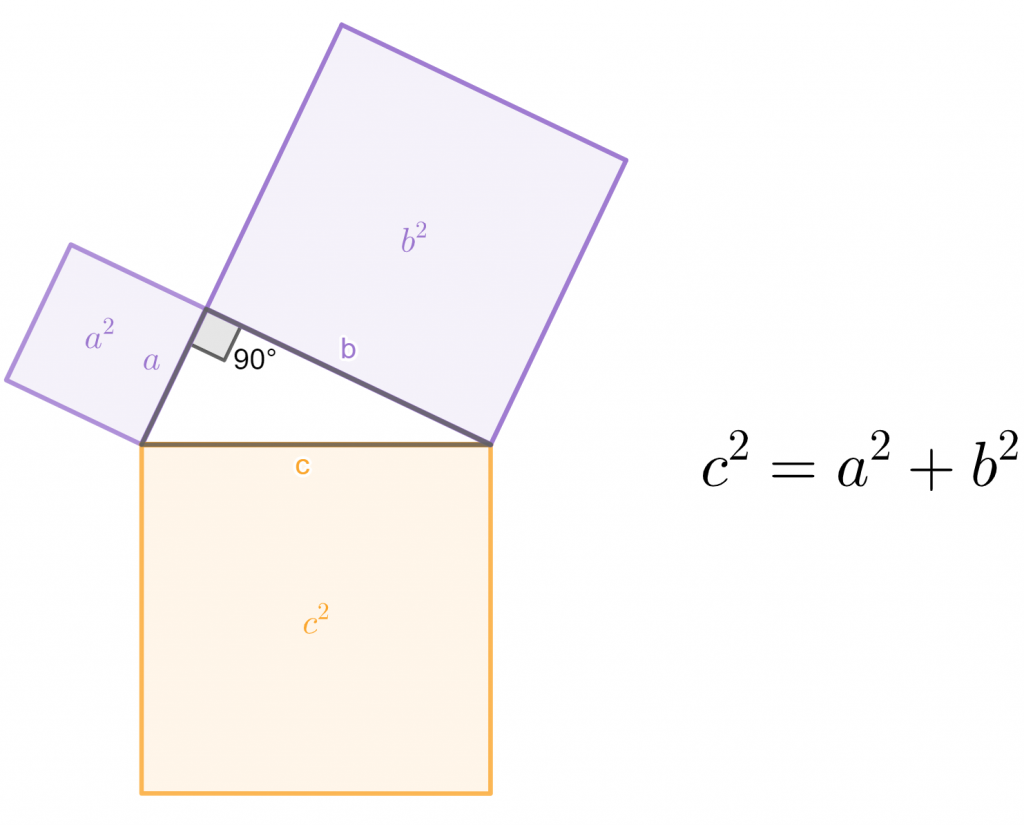
En un triángulo rectángulo, los lados menores son los que forman el ángulo recto y se llaman catetos y el lado mayor se llama hipotenusa. En el triángulo rectángulo de la imagen:
- a y b son los catetos
- c es la hipotenusa
¿Sabes que el teorema de Pitágoras es una de las ecuaciones más importantes para la historia de la ciencia?
Demostraciones del teorema de Pitágoras
El teorema de Pitágoras ha sido demostrado de diversas maneras a lo largo de la historia, y existen numerosas demostraciones. Cada demostración presenta enfoques y conceptos matemáticos diferentes, a continuación vamos a ver tres de ellas:
- Demostración del teorema de Pitágoras utilizando regletas de Montessori.
52=32+42
25=9+16
25=25
- Demostración del teorema de Pitágoras utilizando las piezas del Tangram.
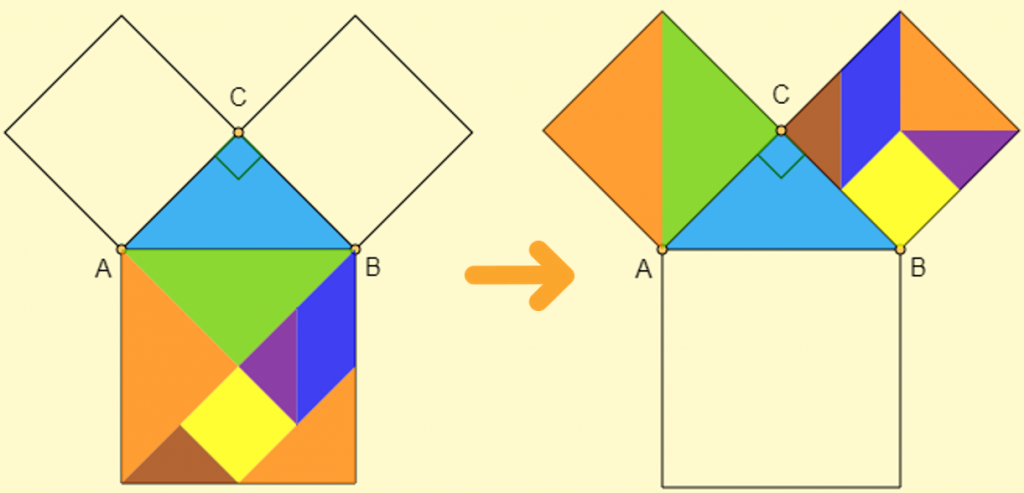
En el siguiente vídeo puedes ver la demostración interactiva:
- Demostración del teorema de Pitágoras de Perigal. Al matemático inglés Henry Perigal (1801/1898), se le atribuye una ingeniosa comprobación del teorema de Pitágoras. «Sobre el mayor de los cuadrados construidos sobre los catetos se determina el centro y se trazan dos rectas paralela y perpendicular a la hipotenusa del triángulo. Con las cuatro piezas obtenidas más el cuadrado construido sobre el otro cateto podemos cubrir el cuadrado construido sobre la hipotenusa.»
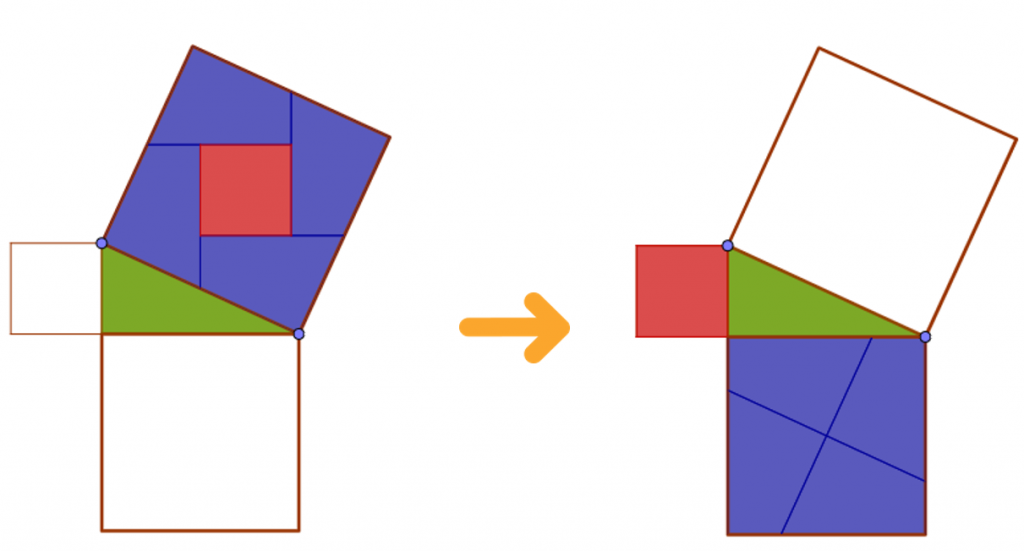
En el siguiente vídeo puedes ver la demostración interactiva:
Resolver problemas utilizando el teorema de Pitágoras
Después de haber visto qué es el teorema de Pitágoras y algunas de sus demostraciones, vamos a ver un ejemplo de un problema que se resuelve utilizando el teorema de Pitágoras.
Enunciado del problema:
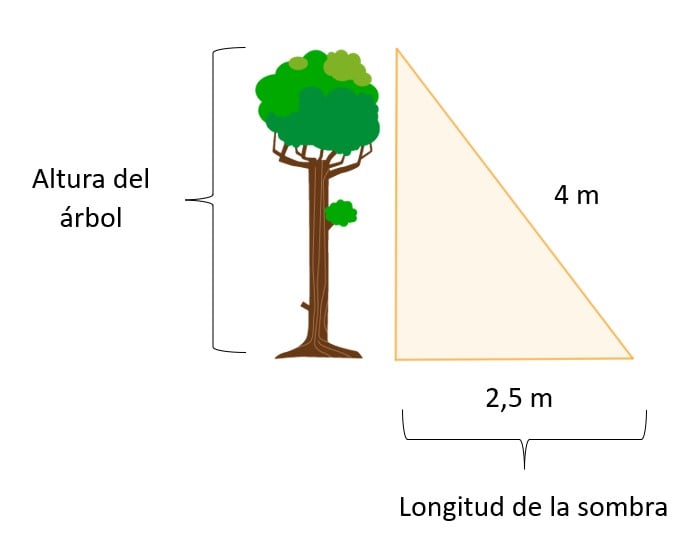
Queremos medir la altura de un árbol. A cierta hora del día, notamos que la sombra del árbol en el suelo mide 2,5 metros. Además, medimos la distancia desde la punta del árbol hasta el final de la sombra en el suelo, y esa distancia es de 4 metros. ¿Cuál es la altura aproximada del árbol?
Resolución del problema aplicando el teorema de Pitágoras:
Para calcular la altura del árbol, podemos usar el teorema de Pitágoras. En este caso, debemos identificar qué lados del triángulo rectángulo formado por la sombra, el árbol y la distancia que une sus puntas tenemos. Desde ahora, nos permitimos asumir que el árbol es perfectamente recto si no, el triángulo ya no sería rectángulo y no podríamos utilizar el teorema de Pitágoras.
La altura del árbol y la longitud de la sombra son los catetos del triángulo rectángulo y la distancia entre el punto más alto del árbol y la sombra sería la hipotenusa.
- a es la altura del árbol
- b es la longitud de la sombra
- c es la distancia desde la punta del árbol hasta el final de la sombra
c2=a2+b2
42=a2+(2,5)2
a2=42-(2,5)2
a=3,12
Así que, la altura del árbol aproximada es 3,12 metros. Para enfrentarse a este tipo de problemas es necesario saber resolver ecuaciones cuadráticas y recordar cómo redondear números decimales.
Espero que este post te haya resultado interesante, no dudes en compartirlo o en escribir en comentarios tus dudas, cuestiones, o los temas de los que te gustaría saber más. Para seguir aprendiendo, registrate en Smartick, el método online de aprendizaje de matemáticas y comprensión lectora para niños de 4 a 14 años.
Para seguir aprendiendo:
- Curiosidades de algunas figuras geométricas
- Las ecuaciones más importantes para la historia de la ciencia
- Propiedad conmutativa de la multiplicación y de la suma
- Ubicar los diferentes números en la recta numérica
- Propiedad distributiva de la multiplicación
Es además monitora de ocio y tiempo libre.
Forma parte del equipo de didáctica de Smartick, le gusta transmitir conocimientos y valores a los demás y aprender.
Siente curiosidad por lo desconocido, le encanta pasar tiempo con sus seres queridos y viajar.