En esta entrada vamos a ver qué es una balanza y su importancia en la lógica matemática. También veremos algunos ejercicios de balanzas que aparecen en las sesiones de Smartick y, por último, la utilidad de las balanzas para entender el signo del igual como equivalencia en ecuaciones algebraicas.
Índice
¿Qué es una balanza?
Una balanza es una herramienta que nos ayuda a comparar y medir el peso de diferentes objetos. Enseñar conceptos como el equilibrio, la medición de pesos y las equivalencias mediante el uso de balanzas desempeña un papel crucial en el desarrollo de la lógica matemática. Además, la utilización de esta herramienta proporciona una representación visual de la igualdad, permitiendo comprender de manera concreta cómo dos lados son iguales cuando están equilibrados, lo que es esencial para la comprensión de ecuaciones matemáticas.
Por otro lado, trabajar con balanzas fomenta habilidades de resolución de problemas al enfrentarse a cómo equilibrar una balanza. Este enfoque práctico también facilita la aplicación de operaciones matemáticas, como la suma y la resta, al mostrar cómo añadir o quitar peso afecta el equilibrio.
La función principal de una balanza es comparar pesos. Al colocar objetos en ambos lados de la balanza, se puede determinar cuál es más pesado, más ligero o si ambos tienen el mismo peso. Esto facilita la comparación relativa de diferentes cantidades de materia. Imagina dos platos, uno en cada uno de los dos extremos de una barra horizontal. Puedes colocar un objeto en un plato y otro objeto en el otro plato. Si un lado baja más que el otro, significa que ese objeto es más pesado. Si ambos lados están al mismo nivel, ¡los dos objetos tienen el mismo peso!
Cuando ambos platillos de la balanza están al mismo nivel, indica que los pesos son iguales. Este concepto de equilibrio es fundamental y tiene aplicaciones prácticas en la resolución de problemas de peso y en la igualdad de cantidades.
Balanzas en ejercicios de Smartick
Ahora, vamos a ver dos ejercicios de balanzas que aparecen en las sesiones de Smartick.
Ejemplo 1
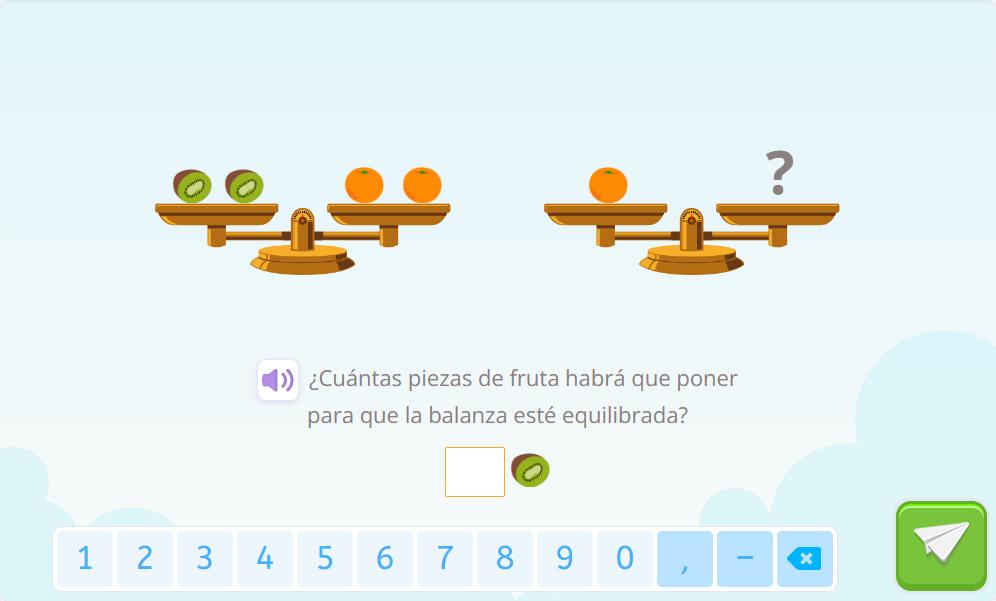
Hay que fijarse en los platos de la primera balanza del ejercicio y buscar la relación que hay entre el peso de los objetos de un plato y el peso de los objetos del otro plato. La primera balanza está en equilibrio cuando en el plato de la izquierda hay dos kiwis y en el de la derecha hay dos naranjas. Esto quiere decir, que un kiwi pesa lo mismo que una naranja.
Ahora queremos ver cuántos kiwis hay que poner para que la segunda balanza esté en equilibrio, vamos a fijarnos en las frutas del plato izquierdo. Hay solo una naranja y hemos visto que el peso de una naranja equivale al peso de un kiwi. Por lo que, para que la segunda balanza esté equilibrada solo hay que poner un kiwi.
Ejemplo 2
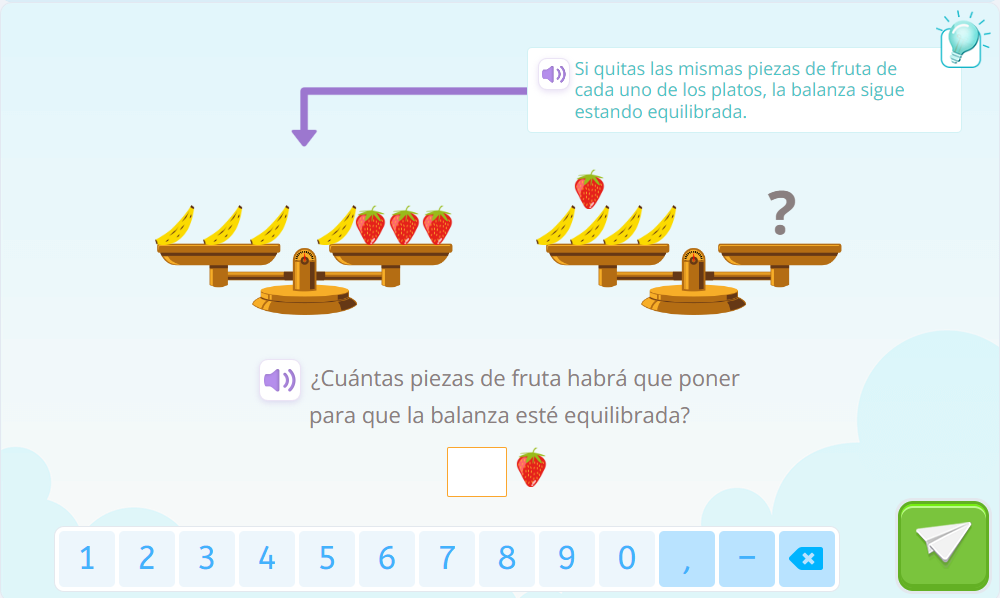
De nuevo, hay que fijarse en los platos de la primera balanza del ejercicio y buscar la relación que hay entre el peso de los objetos de un plato y el peso de los objetos del otro plato. ¡Fíjate! En este ejercicio hay una pista, dice lo siguiente: “Si quitamos las mismas piezas de fruta de cada uno de los platos, la balanza sigue estando equilibrada.” En este caso, eliminamos un plátano del plato de la izquierda y un plátano del plato de la derecha. Al eliminar las piezas que tenían en común ambos platos, vemos que el peso de dos plátanos, equivale al peso de tres fresas.
Entonces, si ahora queremos ver cuántas piezas de fruta hay que poner para que la segunda balanza esté equilibrada, tenemos que fijarnos en las frutas del plato de la izquierda. Hay cuatro plátanos y una fresa, como hemos dicho que dos plátanos equivalen a tres fresas, entonces cambiamos los cuatro plátanos por seis fresas y como la balanza tiene que estar equilibrada, hay que añadir una fresa más. En total hay que poner 7 fresas.
Ahora que has visto dos ejemplos, ¿te atreves a enfrentarte al siguiente ejercicio propuesto?
Ejercicio propuesto
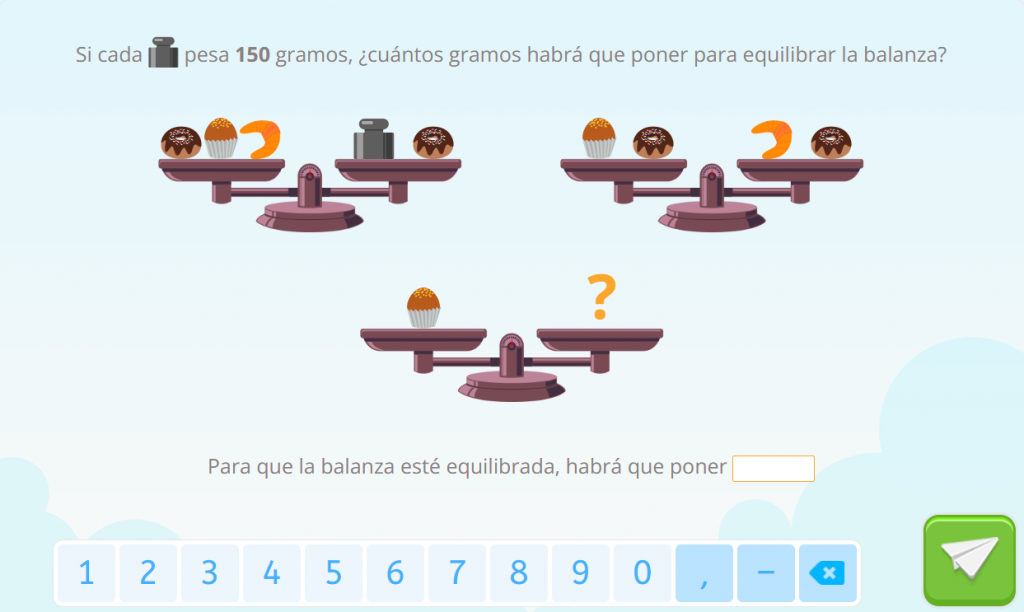
Solución del ejercicio propuesto: 75 gramos.
Balanzas y ecuaciones algebraicas
Como hemos dicho antes, las balanzas permiten la visualización de ecuaciones algebraicas mediante la analogía con el equilibrio en una balanza.
Hasta que no entramos en contacto con el álgebra, siempre vemos el signo igual como algo que nos indica una operación que debemos realizar. Sin embargo, cuando nos enfrentamos a una ecuación y vemos dos lados que no están directamente relacionados por una operación aritmética, entender el nuevo significado de igualdad como un equilibrio para un valor específico puede resultar complicado. Ahora, el igual no es una instrucción, sino un concepto de equilibrio que solo se mantiene para un valor particular de una letra.
Ahí es donde las balanzas entran en juego. Nos ayudan a comprender este nuevo significado del signo igual. Necesitamos ver el igual como un equilibrio, y las balanzas se convierten en una herramienta increíble para entender este nuevo sentido de equilibrio. Entonces, ¿quién hubiera pensado que las balanzas podrían ser clave para entender el álgebra y el intrigante mundo de las ecuaciones?
Vamos a ver un ejemplo de cómo podemos representar una ecuación de primer grado simple con una balanza. Para ello, utilizaremos la herramienta gratuita «balanza» de Mathigon , puedes encontrarla en la sección de Álgebra. Fíjate, en la siguiente imagen podemos ver una analogía de la ecuación 2x+2=8 con una balanza: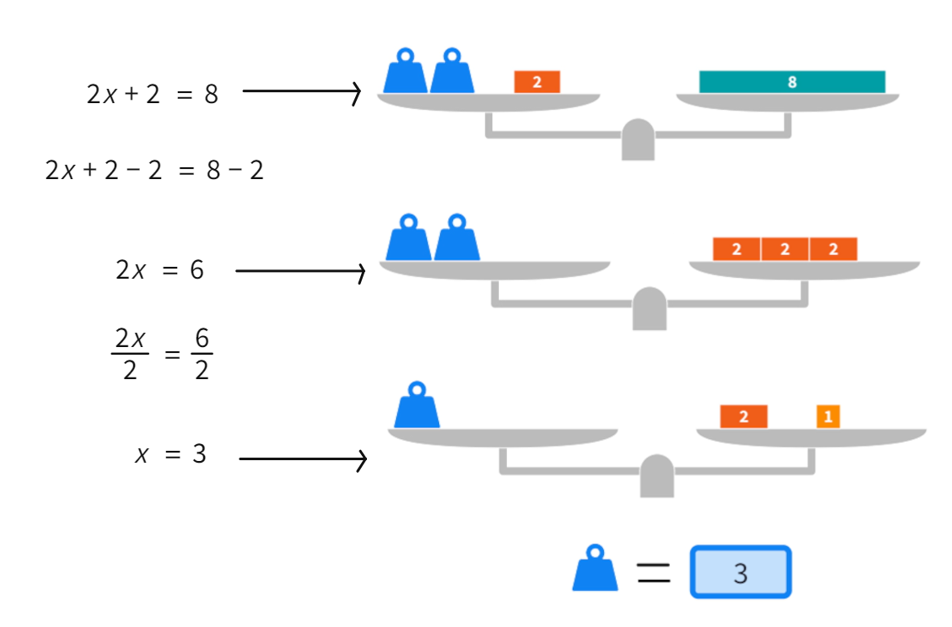 
En el siguiente vídeo puedes ver cómo se resuelve la ecuación paso a paso con una balanza:
Puedes intentar resolver con balanzas las ecuaciones que tienen como ejemplo en esta página de Mathigon.
Espero que este post te haya resultado interesante, no dudes en compartirlo o en escribir en comentarios tus dudas, cuestiones, o los temas de los que te gustaría saber más. Para aprender más, registrate en Smartick, el método online de aprendizaje de matemáticas y comprensión lectora para niños de 4 a 14 años.
Para seguir aprendiendo:
- Acertijo matemático para las vacaciones. ¿Te animas a resolverlo?
- Introducción a las ecuaciones: Cómo resolverlas fácilmente con ejemplos
- Barras de Singapur aplicadas a la resolución de ecuaciones algebraicas I
- Ecuaciones reducibles: ¿qué son? ¿cómo se resuelven?
- Por qué son importantes los ejemplos en la enseñanza de las matemáticas
Es además monitora de ocio y tiempo libre.
Forma parte del equipo de didáctica de Smartick Matemáticas, le gusta transmitir conocimientos y valores a los demás y aprender.
Siente curiosidad por lo desconocido, le encanta pasar tiempo con sus seres queridos y viajar.