Seguro que estás acostumbrado a escuchar frases como «es lógico que la carretera esté mojada» o «lo que Aitana ha dicho tiene lógica». En ambas frases,el término ‘logic@’ parece indicar que existe algo más que no se ha dicho y que hace razonable un determinado hecho. Entonces, ¿podemos decir que la lógica es lo razonable? ¡Vamos a verlo!
¿Qué es la lógica?
Disciplinas como las matemáticas, la lingüística, el derecho, la física o la informática tienen en común la lógica. Por lo tanto, la lógica no es un tema de estudio concreto sino algo que va mucho más allá.
La lógica tiene que ver con las relaciones que hay entre las proposiciones del lenguaje que utilizamos para describir aspectos del mundo que nos rodea. Es importante entender que no cualquier frase es una proposición. En efecto, las proposiciones son frases de las que se puede decir si son o no verdaderas. Por ejemplo, «¿me alcanzas la sal?» no es una proposición porque no tiene sentido afirmar que «¿me alcanzas la sal?» es verdad. Sin embargo, «la carretera está mojada» sí que es una proposición puesto que se puede decir de ella que es verdad si efectivamente hay charcos de agua sobre el asfalto.
En concreto, la lógica se encarga del estudio de la relación de consecuencia entre proposiciones. Pero lo hace una manera muy especial, de una manera muy «matemática». Esto es, la lógica se limita a lo que el lenguaje dice y no a lo que el lenguaje muestra.
Por ejemplo, imagina que te encuentras un problema de matemáticas tradicional como puede ser el siguiente:
A ninguno se le ocurriría decir que quizás Carlos no llegó a comprar los caramelos, o que perdió algunos de los que tenía cuando iba al quiosco. Lo que se hace es poner el foco en las operaciones que aparecen explícitamente en el enunciado. Es decir, 5 caramelos más 7 caramelos.
Con la lógica ocurre algo similar cuando lo que se trata de analizar es la consecuencia de algunas proposiciones. ¡Vamos ahora a comprender qué es eso de la consecuencia!
La consecuencia lógica y su importancia
Vamos a aproximarnos a la noción de consecuencia lógica mediante el análisis de la siguiente actividad:
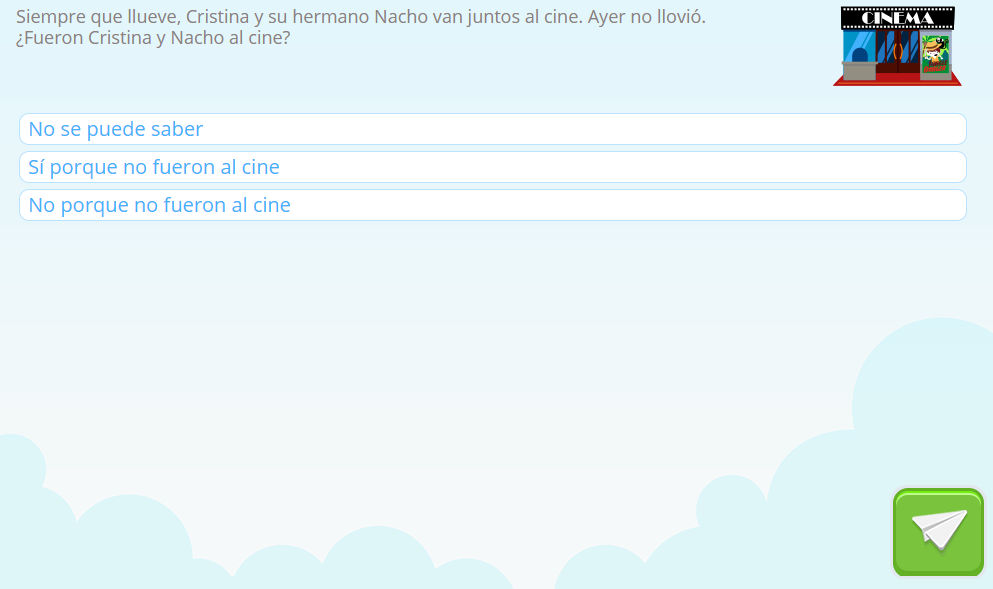
Vamos a llamar p a la proposición «ayer llueve» y q a «Cristina y su hermano Nacho fueron ayer juntos al cine». Lo que el enunciado está afirmando es que si p, entonces q. Además, nos está diciendo que ayer no llovió, esto es, no p. La pregunta que se plantea es si se puede deducir lógicamente no q a partir de si p, entonces q y no p. La respuesta es que no. Vamos a ver por qué.
La forma más elemental de razonamiento lógico y que se remonta hasta la antigüedad es la que se conoce como modus ponendo ponens, que no es más que lo que dicta el sentido común. Si una cosa implica otra y la primera ocurre, pues entonces la segunda también. Dicho de una manera más formal,
si p, entonces q y p, se deduce que q
Sin embargo, no es cierto que de si p, entonces q y no p, se deduzca que no q. En efecto, en el caso del ejemplo, Cristina y Nacho podrían o no haber ido al cine ayer pues lo único que dice el enunciado es que si llueve, entonces van. En cambio, no dice nada sobre lo que hacen o dejan de hacer los días en los que no llueve.
Situaciones como la anterior reflejan el «hacer lógica». En efecto, la lógica vuelve sobre el pensamiento, revisando las relaciones existentes entre lo que sabemos. Así, permite identificar estructuras de razonamiento válidas y detectar aquellas erróneas que conducen a falsos conocimientos sobre el mundo que nos rodea. El estudio de la lógica es vital para la formación completa del niño pues desarrolla su destreza a la hora de argumentar correctamente y, en última instancia, su capacidad de pensamiento crítico.
Te dejamos aquí entradas anteriores del blog de Smartick con más ejercicios de lógica que se pueden encontrar los niños en sus sesiones diarias:
- Ejercicios de operadores.
- Ejercicios de grafos.
- Cinco ejercicios de lógica para practicar este verano.
Y…Si quieres que tu hijo desarrolle su sentido crítico mientras aprende matemáticas, entonces no dudes en unirte a la comunidad Smartick. ¡Regístrate y pruébalo gratis!
Para seguir aprendiendo:
- Diagramas de Venn: Descubre cómo utilizarlos para evaluar argumentos
- Cuarta parte
- Ejercicios de lógica en Smartick
- Ejercicios de lógica en Smartick II
- Por qué son importantes los ejemplos en la enseñanza de las matemáticas
Actualmente está cursando estudios de doctorado en Investigación en educación en la Universidad de Valladolid.
Es profesor de didáctica de la matemática en la Universidad de Valladolid y forma parte del equipo de desarrollo de contenidos de Smartick.
Entre sus aficiones destacan el tenis, el jazz y la escritura.
- Propiedades de las potencias - 13/04/2020
- El porqué de los criterios de divisibilidad - 02/03/2020
- Por qué son importantes los ejemplos en la enseñanza de las matemáticas - 27/01/2020
Felicitaciones por la propuesta de «aprender lógica», pero, ¿por donde empezar con los chicos de primaria? ¿hay alguna bibliografía?
De nuevo muchas gracias por la incitación a aprender a razonar.
Es interesante está materia.me gusta ampliar los conocimientos y que mis hijos conozcan una herramienta importante en su preparación profesional
¡Hola, Ricardo!
En Smartick hemos lanzado Smartick Thinking el programa con el que tus hijos trabajarán lógica, aprenderán a pensar antes de actuar, entrenando habilidades que estimulan su pensamiento crítico, y fortalecen su capacidad para tomar decisiones de forma razonada por sí mismos.
Te invitamos a que os registréis en Smartick Thinking y lo probéis gratis.
¡Un saludo!
Muy brillante tu exposición del razonamiento lógico con dos ejemplos estupendos. Ha sido muy instructivo.