Conoce los números racionales y sus propiedades
27 agosto 2018
En el post de hoy vamos a aprender un poco más sobre los números racionales.
Ya vimos anteriormente en este post cómo representarlos en la recta numérica. Y en este otro post, qué tipos de números racionales existen.
Vamos a conocerlos ahora un poco más en detalle.
Propiedades de números racionales
Los números racionales son aquellos que pueden representarse como cociente de dos números enteros. Es decir, los podemos representar mediante una fracción a/b, donde a y b son números enteros y además b es distinto de cero.
El término «racional» proviene de razón, como parte de un todo (por ejemplo: «Tocamos a razón de tres por persona»).
Cada número racional se puede representar con infinitas fracciones equivalentes. Por ejemplo, el número racional 2.5 se puede representar con las siguientes fracciones:
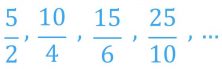
Y con todas las fracciones equivalentes a éstas.
El conjunto de todos los números racionales se representa con el siguiente símbolo:
Fíjate en que cualquier número entero es también un número racional pues puede representarse como cociente de dos números enteros.
Por ejemplo, el número 5 puede representarse con las siguientes fracciones:
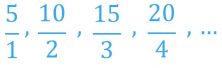
Esto quiere decir que el conjunto de los números enteros está contenido en el conjunto de los números racionales, que matemáticamente se escribe:
Para completar los números de la recta numérica, o números reales, existen números que no pueden representarse mediante el cociente de dos números enteros.
Estos números se denominan números irracionales, y los más conocidos son estos:
Los números racionales en el Antiguo Egipto
Los números racionales surgen con la necesidad de repartir una cantidad D en d partes, donde D no es múltiplo de d.
Para calcular la cantidad que será repartida a cada parte, se necesita realizar la operación D:d, que no tiene como resultado un número entero, ya que D no es múltiplo de d.
Para dar resultado a esta operación, aparecen entonces unos números que pueden representarse de la forma D/d, distintos de los números enteros.
En el Antiguo Egipto hacían ya este tipo de repartos de «las partes de un entero», utilizando casi exclusivamente fracciones unitarias, que son las que tienen numerador 1. Es decir, las que podemos representar mediante una fracción 1/b, donde b es un número entero positivo.
Estas fracciones unitarias las representaban mediante un jeroglífico con forma de «boca abierta» que denotaba la barra de fracción, y un jeroglífico numérico escrito debajo que denotaba el denominador de la fracción.
Por ejemplo, para representar 1/4 lo hacían de la siguiente manera:
Cualquier fracción no unitaria la representaban como suma de fracciones unitarias distintas. De ahí que las sumas de fracciones unitarias se conozcan como fracciones egipcias.
¿Qué te ha parecido este post? ¿Te ha gustado conocer mejor los números racionales? Si es así, compártelo para que otros también puedan aprender sobre ellos.
Y si quieres aprender más matemáticas de primaria, adaptadas a tu nivel de conocimientos, entra en Smartick y pruébalo gratis.
29 Comentarios
Super buena información
Gracias por la información valiosa y práctica.
Gracias, me sirvió para una investigación.
Toda la info es muy buena, me ayudó mucho.
Es muy bueno
Creo que la información que se encuentra en este blog es demasiado impresionante.
Muchas gracias por tu comentario Aslin, nos alegra mucho saber que te sirven de ayuda nuestras entradas del blog. 😊
Excelente
Excelente explicación
Me encanta que se compartan datos curiosos sobre las matemáticas, de verdad que me inspira aprender así, muchas gracias. 💕
Con este método he aprendido mucho
me ha ayudado muchísimo me gusta mucho su sitio web ⭐⭐⭐⭐⭐
Es muy buena esta página
me encanta
muchas gracias por explicarlo…espero que me salga bien mi examen de mates del martes
¡Suerte!
Me ayudó mucho. Muchísimas gracias a quien lo haya publicado.
excelente toda la temática que se maneja para comprender mejor los temas tratados, los ejemplos y sobre todo los ejercicios de cada explicación, felicitaciones
Muy excelente los números racionales.
Excelente su presentación, de fácil comprensión.
me gusta esta página
Me gustó mucho
Me ayudaron mucho en un taller con defensa muchísimas gracias 🙏😍❤️😘
Necesito más
Hola Jonathan:
Si quieres aprender más, te recomiendo probar el método Smartick, en el que con 15 minutos al día trabajas cálculo, lógica, programación y muchas más habilidades. ¡Puedes probar nuestro periodo de prueba gratuito sin ningún tipo de compromiso!
Si tienes cualquier duda puedes contactar con mis compañeras de atención al cliente en [email protected]
¡Un saludo!
Buenos días las matemáticas son muy útil en nuestra vida, sin embargo hay que quitarle el paradigma de que es casi imposible aprender matemáticas. Aunque no es fácil con dedicación puede lograrse. Es mi humilde opinión aunque no soy matemático. Gracias.
Excelente explicación y muy interesante la reseña histórica de los egipcios.
Gracias muchísimas gracias. Me encantó es muy rápido y además muy fácil
Me ha gustado mucho esta página es muy fácil y muy rápida