Las barras de Singapur son un método visual muy útil para entender el concepto de las operaciones aritméticas sencillas. La semana pasada aprendimos cómo se utilizan las barras de Singapur para hacer sumas y restas, y hoy vamos a usarlas para entender la relación entre la multiplicación y división.
Tenemos dos cantidades de forma que una es múltiplo de la otra. A no ser que hayamos multiplicado por 1 (este caso no lo tenemos en cuenta hoy) tendremos una cantidad más grande y otra más pequeña. La relación que hay entre estas dos cantidades es cuantitativa y se llama múltiplo. ¿Cómo encontramos este número? Dividiendo:
Cantidad grande : cantidad pequeña = múltiplo
El múltiplo es el número del que hablamos cuando decimos «el doble de», «el triple de»…
Por ejemplo:
Sergio y Juan se han ido de excursión. Sergio ha hecho 6 fotos y Juan ha hecho 3. ¿Cuántas veces más fotos ha hecho Sergio que Juan?
Primero vemos cuál es la cantidad grande y cuál es la cantidad pequeña:
Cantidad grande: 6
Cantidad pequeña: 3
Dibujamos la barra de Singapur para averiguar qué cantidad entra 3 veces en 6:
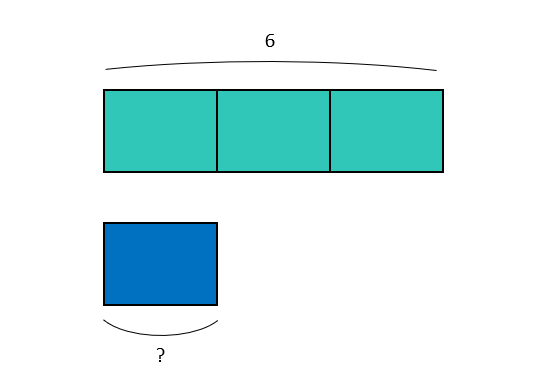
Entonces la operación es 6 : 3 = 2
Es decir, Sergio ha hecho el doble de fotos que Juan.
Imaginemos ahora que en un problema nos dan la cantidad pequeña y queremos hallar la grande. Entonces tenemos que hacer
Cantidad pequeña x múltiplo = cantidad grande
Con las barras de Singapur se entiende perfectamente, lo vemos con un ejemplo:
Juan y Claudia juegan a los dados. Juan ha ganado 4 veces y Claudia ha ganado 5 veces más que él. ¿Cuántas veces ha ganado Claudia?
Cantidad pequeña: 4
Múltiplo: 5
La barra de Singapur correspondiente es:
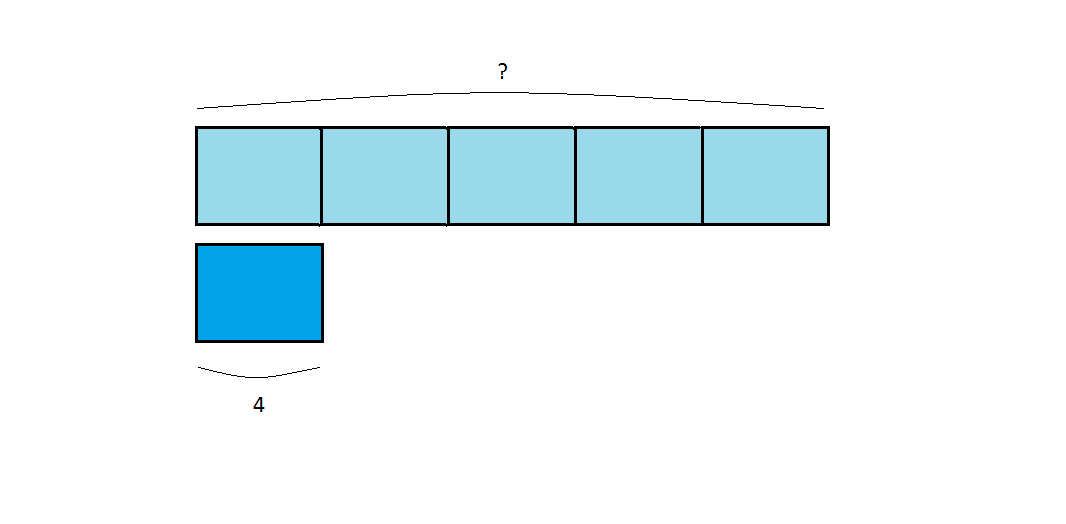
Entonces la cantidad grande es 4 x 5 = 20. Es decir Claudia ha ganado 20 veces.
En este caso, cada unidad de la barra representa 4 victorias de Juan. Poniendo esa misma unidad 5 veces repetida como nos dicen en el enunciado, es fácil ver que tenemos que multiplicar.
Por último, imaginemos que tenemos la cantidad grande y el múltiplo, y queremos hallar la cantidad pequeña. Entonces tenemos que hacer:
Cantidad grande : múltiplo = cantidad pequeña
Igual que antes, es mucho más fácil de verlo con un ejemplo y con una barra de Singapur:
La semana pasada Juan participó en un concurso de cocina y aunque no consiguió ganar obtuvo 28 puntos, 4 veces más que el participante que quedó en último puesto. ¿Cuántos puntos obtuvo en el que quedó el último?
Cantidad grande: 28
Múltiplo: 4
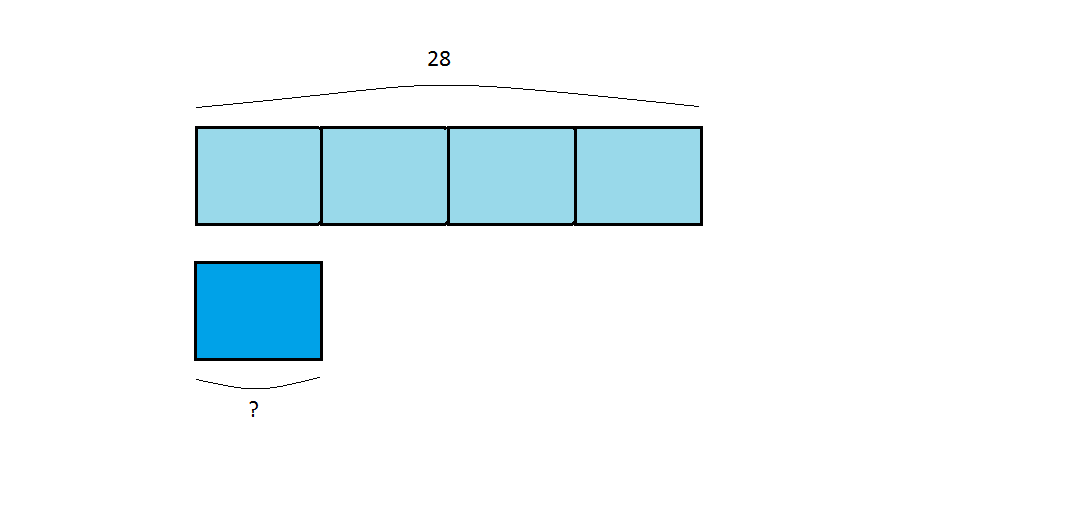
Entonces la cantidad pequeña es 28 : 4 = 7
El que quedó en último lugar consiguió 7 puntos.
En este caso no sabemos cuánto representa la unidad, pero vemos que la cantidad total es 28 y queremos ver en cuánto queda la unidad si queremos dividirlo entre 4 unidades.
¡Ya sabes aplicar las barras de Singapur a la multiplicación y división!
En estas otras entradas de nuestro blog puedes practicar multiplicación y división:
Y si quieres seguir aprendiendo muchas más matemáticas, ¡entra en Smartick, regístrate y pruébalo gratis!
Para seguir aprendiendo:
- Barras de Singapur aplicadas a la resolución de problemas II
- Barras de Singapur aplicadas al concepto de porcentaje
- Barras de Singapur aplicadas a la suma y resta
- Barras de Singapur aplicadas a las fracciones
- Barras de Singapur aplicadas a la resolución de problemas
Actriz de teatro empedernida y gran aficionada a la fotografía. Si consigue algo de tiempo, observa las estrellas.
- Figuras geométricas. Clasificación, tipos y ejemplos - 20/03/2017
- Nuevos contenidos de Smartick - 11/07/2016
- Ejercicios de lógica en Smartick II - 23/06/2016
Buenas estrategias para las matemáticas ,felicitaciones.
excelentes ideas que contribuyen en el aprendizaje de matemáticas.