Para resolver problemas de medidas de tiempo, primero debemos conocer cuáles son las unidades de medida de tiempo y sus equivalencias.
Si ya lo sabes, puedes continuar leyendo esta entrada y si no, puedes hacer clic en este enlace para recordarlo.

Como se puede ver en la tabla de arriba, hay unidades mayores que el día y hay otras menores. Las menores son la hora, el minuto y el segundo, y forman parte de un sistema sexagesimal. Esto quiere decir que van de 60 en 60, así una hora son 60 minutos y 1 minuto son 60 segundos.
1 h = 60 min 1 min = 60 s 1 h = 3600 s
También es importante recordar que las medidas de tiempo (sistema sexagesimal) pueden expresarse de dos formas:
- Forma incompleja: utilizando una sola unidad. Por ejemplo: 8640040 s
- Forma compleja: utilizando varias unidades a la vez. Por ejemplo: 2 h 20 min 40 s. En una expresión compleja la cantidad de minutos y segundos siempre tiene que ser inferior a 60.
¿Es posible pasar una medida de una forma a otra?
La respuesta es sí. Una medida en forma compleja puede escribirse en forma incompleja y viceversa. Veamos cómo podemos hacerlo.
De forma compleja a incompleja:
Hay que convertir cada parte de la expresión a una misma unidad (la que nos pidan) y luego sumar los resultados.
Expresa 2h 25 min 15 s en segundos.
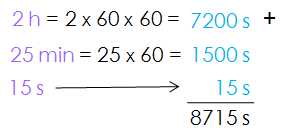
2 h 25 min 15 s = 8715 s
De forma incompleja a compleja:
Hay que dividir la medida y el cociente sucesivo (en caso de ser necesario) entre 60.
Expresa 8715 s en forma compleja
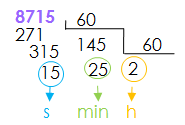
8715 s = 2h 25 min 15 s
En el ejemplo vemos que el resto de la primera división son los segundos de la nueva expresión y el cociente (los minutos) se volvió a dividir entre 60. El cociente de la segunda división son las horas y el resto los minutos.
Con esta información ya podemos resolver el siguiente problema:
El tiempo total del ganador de la carrera de karts escolar fue de 1h 53 min 58 s. El último clasificado entró a 365 s del primero. ¿Cuál fue su tiempo total de carrera? Expresa el resultado en forma compleja.
Vemos que el tiempo del ganador está expresado en forma compleja y la diferencia con el último clasificado está en forma incompleja. Como nos piden el resultado en forma compleja, lo primero que tenemos que hacer es convertir 365 segundos a forma compleja.
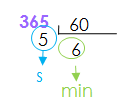
Para convertir 365 segundos a forma compleja empezamos dividiendo entre 60. El resto de la división serán los segundos y el cociente son los minutos, y como es menor que 60 ya no tenemos que seguir dividiendo.
365 s = 6 min 5 s
El segundo paso es sumar para descubrir el tiempo total de carrera del último clasificado:
Sumamos los segundos con los segundos, los minutos con los minutos y las horas con las horas. El resultado es: 1h 59 min 63 s
¿Hemos terminado?
¡Aún no! Recuerda que en una expresión compleja de una medida de tiempo, ni la cantidad de segundos ni la de minutos puede ser superior o igual a 60. Así que nos queda un tercer paso:
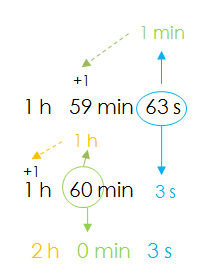
63 s = 60 s + 3 s y 60 s = 1 min, por lo tanto 63 s lo escribimos como 1 min y 3 s.
Ese minuto adicional se lo sumamos a los 59 minutos que ya teníamos y nos queda 1h 60 min 3 s.
Ahora tenemos 60 min y 60 min = 1 h
Por lo tanto, 1 h 60 min 3 s = 2 h 0 min 3 s
Y finalmente tenemos la respuesta expresada en forma compleja: El tiempo total del último clasificado fue de 2 h 0 min 3 s
Una última pregunta antes de terminar…
¿Será válida la expresión 1 min 30,132 s?
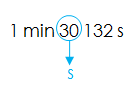
Aunque no es muy común, sí es una expresión válida. De hecho fue el tiempo de clasificación de Fernando Alonso (piloto de Fórmula 1) en el gran premio de Australia del año 2014. Tardó 1 minuto, 30 segundos y 132 milésimas de segundo en dar la vuelta al circuito.
Las décimas, centésimas y milésimas de segundo (submúltiplos del segundo) se emplean cuando es necesario medir el tiempo de una forma mucho más precisa, como en las carreras de fórmula 1.
Si conoces más situaciones en las que se utilicen los submúltiplos del segundo, no dudes en comentarlas. Y recuerda que puedes entrar en Smartick si quieres saber más sobre las medidas de tiempo.
¡Feliz matesemana!
(Una semana son 7 días, o 168 horas, o 10080 minutos, o 604800 segundos, o incluso 604800000 milésimas de segundo)
Para seguir aprendiendo:
- Medidas de tiempo. ¿Qué unidades utilizamos para medir el tiempo?
- Problemas con medidas de tiempo
- ¿Qué son los números decimales?
- Relojes y ángulos
- Ángulos explicados con la ayuda de un reloj
- Aprendiendo matemáticas en educación infantil - 18/11/2019
- «Matemáticas, la base de todas las ciencias» - 17/08/2017
- Propiedades de la suma: conmutativa, asociativa y elemento neutro - 04/02/2016








Está súper bien.
está muy bien
Gracias por el claro contenido.
Hola, quería agradecer a los creadores y creadoras de esta web, me ha sido de gran utilidad ya que antes no entendía nada acerca de este contenido del sistema sexagesimal, tenía un examen pronto sobre esto e iba a suspender seguramente. Mil gracias, ahora lo comprendo mucho mejor y sé realizar operaciones. Animo a la gente a usar smartick, ¡es genial!
¡Gracias!
¡Adoro! No entendía nada y ahora, gracias a vosotros, si. Gracias.
Gracias a vosotros y a vosotras pude porfin entenderlo muchas gracias.
Gracias!!! Muy bien explicado …. Un Saludo :3
Hola, me gusta mucho
Buenos días, muy bien expuesto, todo muy claro y con buenos ejemplos. No obstante permitidme comentar que se os ha colado un pequeño gazapo en el último ejemplo.
Si es válida la expresión. 1 min 30 132 s.
Entiendo que falta la coma, en primer lugar, entre 30 y 132. Y sobre todo: Las unidades : 1 centésima, 3 décimas y 2 milésimas. Cuando debería de ser 1 décima, 3 centésimas y 2 milésimas. Saludos
Hola Agustín Emilio:
Muchísimas gracias por seguirnos y por tu comentario, ya hemos modificado el error en el post.
Un saludo!
Una explicación perfecta.
gracias por todo¡¡¡¡¡¡¡¡