En una entrada anterior de nuestro blog veíamos cómo la mejora de la comprensión lectora mejoraría las competencias matemáticas. Y nos proponíamos retomar el tema del importante papel de los problemas verbales y sus implicaciones en la enseñanza-aprendizaje de las matemáticas.
En Smartick, siempre decimos que un niño que sabe matemáticas es un niño que sabe resolver problemas. ¿Por qué? Porque en la resolución de problemas (de verdaderos problemas) se ponen en marcha procesos muy ricos que van mucho más allá de aplicar una fórmula matemática. ¡Veámoslo!
Siguiendo a Juidías y Rodríguez (2007) el modelo más clásico de las fases por las que atraviesa la Resolución de Problemas Matemáticos (RPM) es el que describe Polya en How to Solve it en 1945. Este proceso para él consta de 4 fases:
1. Comprensión del problema
Comprender un problema supone que entendemos lo que el enunciado nos está diciendo, qué nos pide, cuál es el problema a resolver. Desde Smartick, para fomentar esta comprensión del problema matemático queremos crear problemas que sean realmente para los niños, es decir, ajustarnos al contexto y a los situaciones reales que ellos pueden vivir.
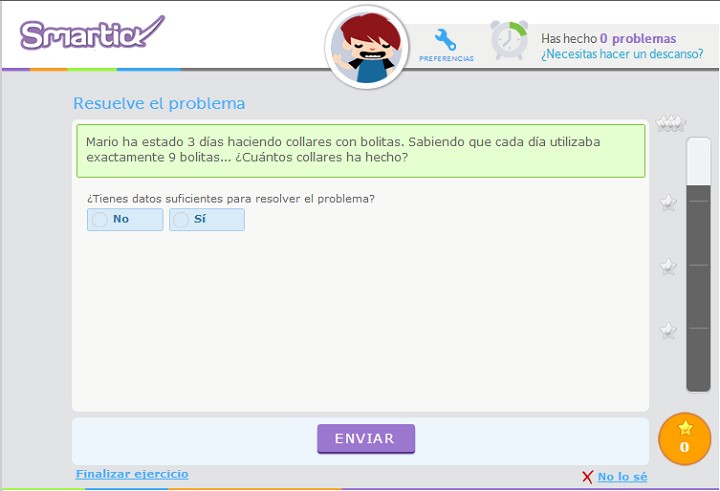
2. Planificación / Elaboración de un plan
Uno planifica algo (un viaje, por ejemplo) cuando tiene claro el objetivo, pero todavía desconoce el camino. El alumno, una vez que ha comprendido el problema ha de enfrentarse a las estrategias que conoce (ejemplos: reducir lo complicado a lo simple, hacer un dibujo que ayude a visualizar la situación, buscar semejanzas con problemas que haya resuelto anteriormente, etc.). Los problemas de Smartick siempre quieren hacer preguntas que obliguen a planificar un plan específico para cada situación, no una simple operación.
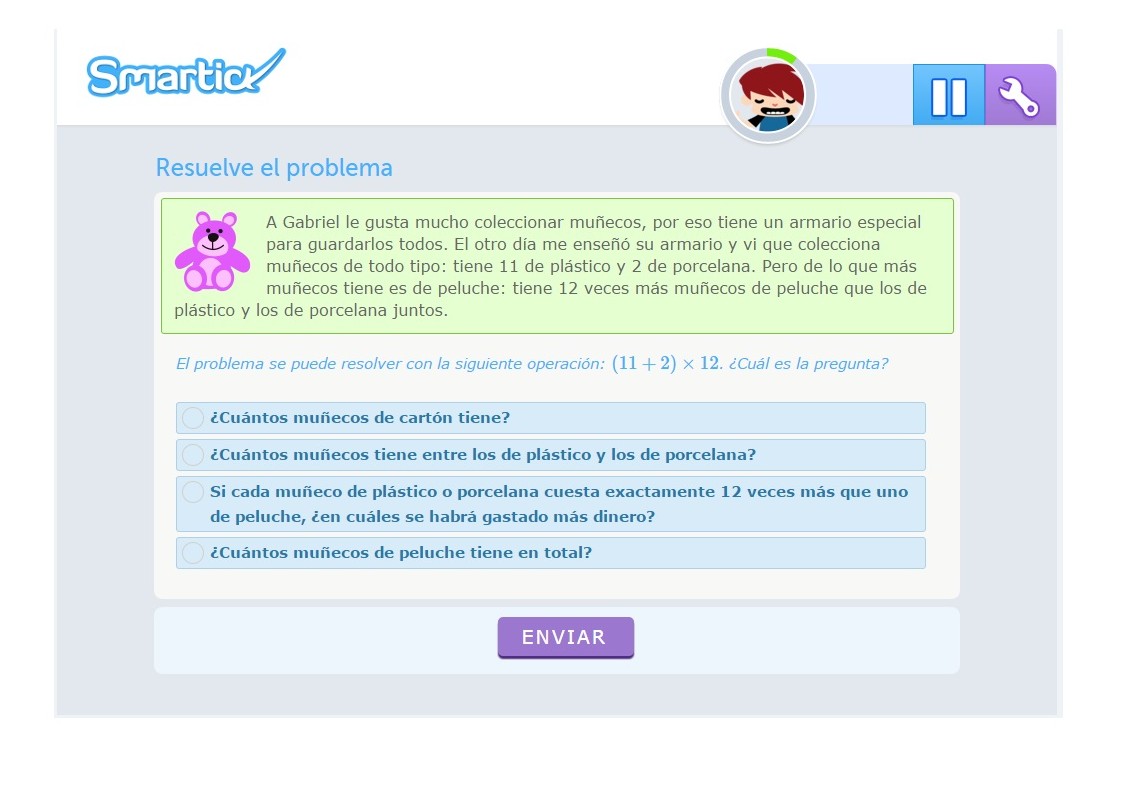
3. Ejecución del plan
Este es el momento de cumplir el plan propuesto para alcanzar nuestro objetivo. Hay que llevarlo a cabo con determinación, con confianza en lo que uno ha pensado. Para ello, es muy interesante trabajar con problemas que pueden resolverse por varios caminos, y todos ellos correctos, o problemas que sean de pregunta cualitativa, que impliquen procesos distintos a un simple algoritmo matemático. Esto puede fomentar en el alumno el interés de encontrar el mejor camino para llegar a la solución, en vez de preocuparse solo por la respuesta correcta.
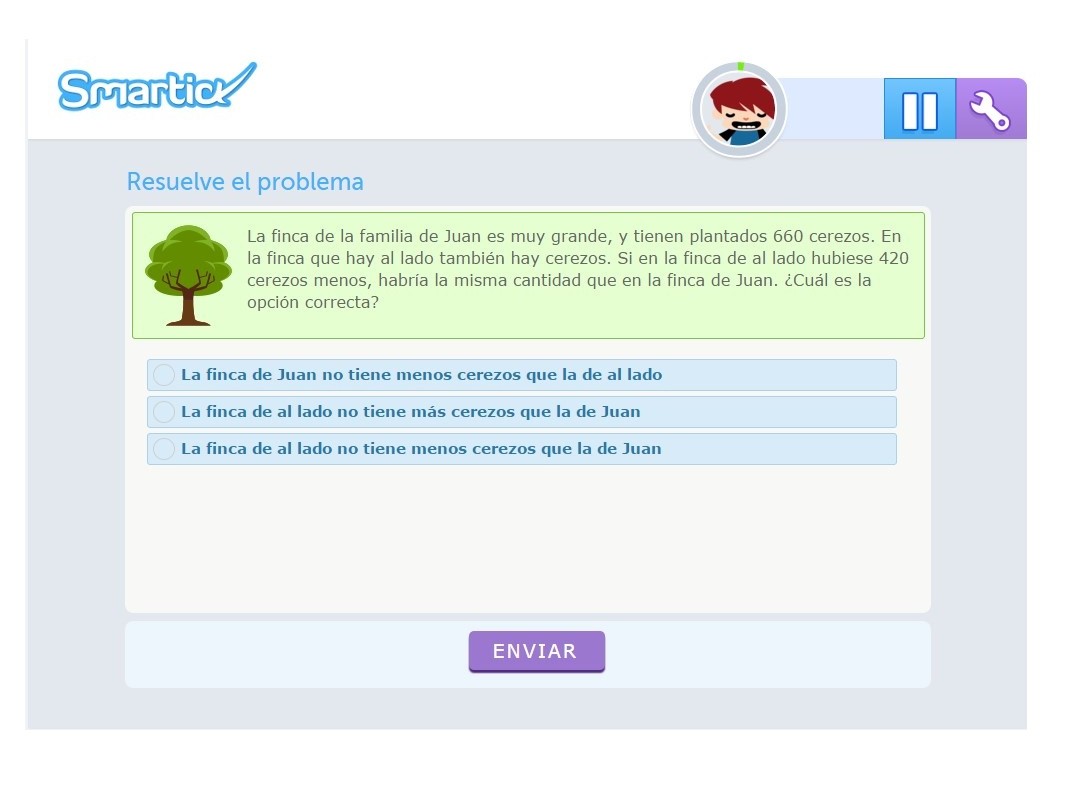
4. Supervisión
¿Ha ido bien o ha ido mal? Para que el aprendizaje sea significativo hay que dar feedback inmediato al alumno, de manera que compruebe en qué ha fallado, y cómo podría haberlo hecho mejor. Para ello, Smartick le da al alumno feedback inmediato y, además, la posibilidad de visitar un vídeo tutorial para aprender más despacio cómo elaborar la estrategia la siguiente vez.
Si quieres aprender matemáticas de primaria adaptadas a tu nivel, date de alta ahora mismo en Smartick y pruébalo gratis.
Referencias:
- Llinares, S. (2008). Agendas de investigación en Educación Matemática en España: una aproximación desde» ISI-web of knowledge» y ERIH.
- Polya, G. (2014). How to Solve It: A New Aspect of Mathematical Method: A New Aspect of Mathematical Method. Princeton university press.
Para seguir aprendiendo:
- Barras de Singapur aplicadas a la resolución de problemas II
- Resolución de problemas de matemáticas
- Problemas matemáticos: Importancia y cómo resolverlos
- Problemas con regla de tres simple
- Problemas de medidas de longitud
Pedagoga a tiempo parcial y lectora de temas educativos a tiempo completo.
Tania coordina la vertiente académica-científica de Smartick con la Universidad y se esmera por descubrir las necesidades de las familias Smartick.
Su pasión son los viajes al extranjero.
hola yo quisiera resolber este problema en un restaurant los comensales estaban sentado 8 en cada mesa al notar que estaban muy junto se trajeron 6 mesas mas entonse a hora hay 5 en cada mesa cuanto semensales hay?
yo era muy mala para las matematicas,pero ahora soy la mas inteligente de mi salon