En posts anteriores hemos tratado regla de tres, esa forma breve de calcular un cuarto número en presencia de otros tres. También qué es un porcentaje y cómo se calcula, en esta entrada vamos a refrescar la memoria y a resolver los casos más importantes de cálculo de porcentaje con reglas de tres.
Índice
Cómo calcular reglas de tres
Los porcentajes o tantos por ciento son una de las formas en las que se puede dar una fracción. Por ejemplo, la fracción cuatro quintos (\(\frac{4}{5}\)) se puede expresar también como tanto por ciento.
Para ello hay que buscar una fracción equivalente con denominador 100, algo que se consigue amplificando la fracción, multiplicando numerador y denominador por 20. Vemos que la fracción (\(\frac{4}{5}\)) es equivalente a (\(\frac{80}{100}\)). Otra forma de nombrar esta fracción es en forma de tanto por ciento, en este caso 80%.
En el otro sentido, siempre que veas un porcentaje, 25%, por ejemplo, puedes imaginártelo como una fracción con numerador 25 y denominador 100. Como esa fracción es equivalente a la fracción \(\frac{1}{4}\) puedes hacer la relación de que el 25% equivale a un cuarto, porque así es.
Por otro lado, la regla de tres se usa como una forma abreviada de calcular un cuarto número en presencia de otros tres cuando sabemos que hay una relación de proporcionalidad entre magnitudes. Simplificando mucho, si sé que dos fracciones, con sus dos numeradores y sus dos denominadores son equivalentes pero no conozco uno de esos cuatro números puedo aplicar la regla de tres para calcular su valor.
En esta entrada vamos a ver cómo hacer una regla de tres en el caso de los porcentajes o tantos por ciento, algo útil en muchos contextos, como cuando, por ejemplo, tenemos que calcular un descuento.
¿Cómo se hace la regla de tres simple?
La regla de tres es el cálculo de un 4º número en presencia de otros tres (cuando sabemos que se da una relación de proporcionalidad. El caso más sencillo de todos es cuando tenemos dos fracciones que sabemos que son equivalentes pero solo conocemos tres de esos números, veamos este ejemplo de regla de tres simple:
\(\huge \frac{20}{60}=\frac{5}{x}\)
Siempre que hay fracciones equivalentes se va a dar que sus productos cruzados valen lo mismo:
\(\large 20·x=60·5\)
Si veinte veces equis vale algo es porque equis vale ese algo entre veinte:
\(\Large x=\frac{60·5}{20}\)
El valor desconocido (quince, en este caso) estaba en el denominador de la segunda fracción, pero si hubiera estado en alguna otra posición, el calculo hubiera sido muy parecido, por ejemplo:
\(\huge \frac{x}{16}=\frac{5}{40}\)
Aplicamos, otra vez, equivalencia de fracciones:
\(\large 40·x=5·16\)
Para obtener que:
\(\Large x=\frac{5·16}{40}\)
Que tiene como solución en este caso el valor dos.
Como vemos la regla de tres en el caso de equivalencia de fracciones es muy sencilla, ¿será siempre así?
Inconvenientes
Cada vez que tengamos una situación expresada como fracciones equivalentes vamos a poder aplicar esta regla, esto hace que se utilice muchísimo, porque son muchos los problemas que se pueden expresar como fracciones equivalentes. Hasta las relaciones de proporcionalidad compuesta o inversa se pueden expresar en términos de fracciones equivalentes.
El mayor inconveniente al aplicar la regla de tres es cuando la relación no está dada como fracciones equivalentes y las magnitudes no se identifican correctamente, o, peor aún, cuando se aplica sin criterio en casos en los que hay proporcionalidad inversa, o no hay proporcionalidad.
Regla de tres en porcentajes
El caso que nos ocupa en esta entrada es siempre de proporcionalidad directa, y no va a ser muy complicado llegar a las fracciones equivalentes, teniendo en cuenta que el porcentaje, como decíamos más arriba, es ya una forma de dar una fracción.
Vamos a ver varios ejemplos de problemas, de los muchos que hay en los que se utiliza correctamente la regla de tres para resolver diferentes tipos de problemas relacionados con porcentajes. El caso más sencillo es en el que conocemos la parte y el todo.
Regla de tres para calcular el porcentaje que representa una cantidad sobre otra
¿Qué porcentaje de 250 representa 50?
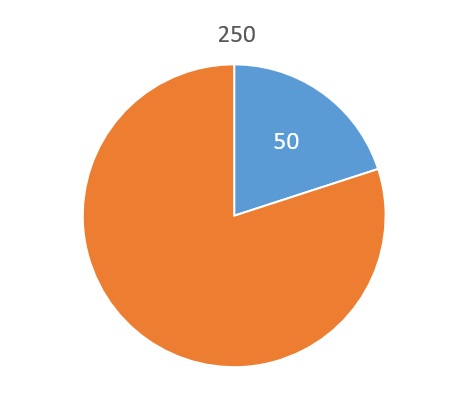
Lo que no conocemos esta vez es el numerador de la fracción con denominador 100, la otra fracción viene dada por las cantidades del enunciado:
\(\huge \frac{x}{100}=\frac{50}{250}\)
Por equivalencia de fracciones:
\(\large 250·x=50·100\)
Que conduce a que
\(\large x=\frac{50·100}{250}=20\)
50 es el 20% de 250.
Este mismo ejemplo, ligeramente modificado, nos resolvería el caso en el que conociésemos que una cantidad se ha visto modificada por un porcentaje, calcular el porcentaje conocidas la cantidad inicial y la cantidad final es muy sencillo. Imagina que sabemos que un producto vale ahora 485 euros, y valía antes 520. El valor actual representa, aproximadamente:
\(\huge \frac{480}{520} \large\approx{0,9231}\)
Ese número decimal es casi el porcentaje, recuerda que el porcentaje es el numerador de una fracción de denominador 100, en nuestro caso:
\(\huge \frac{480}{520}\approx \frac{92,31}{100}=\large{92,31\%}\)
Por lo que podemos decir que a la cantidad inicial, 520, se le ha aplicado un descuento del 7,69%.
Imagina que aparecen las mismas cantidades, solo que en orden inverso, algo que valía 480 euros vale ahora 520, ¿qué incremento se ha aplicado?
Lo primero es identificar cuál es el total, el denominador de la fracción, es 480, porque ese era el cien por cien. Esto es el resultado va a estar por encima de 100%:
\(\huge \frac{520}{480} \large\approx{1,08333…}\)
Como antes, bastará con escribir ese número decimal como una fracción con denominador 100:
\(\huge \frac{520}{480}\approx \frac{108,33}{100}=\large{108,33\%}\)
La nueva cantidad, 520, es el 108,33% de la inicial, por lo que podemos decir que la inicial, 480, se ha incrementado en un 8,33%.
Regla de tres para calcular el porcentaje de un número
Por ejemplo, queremos calcular el 30% de 360.
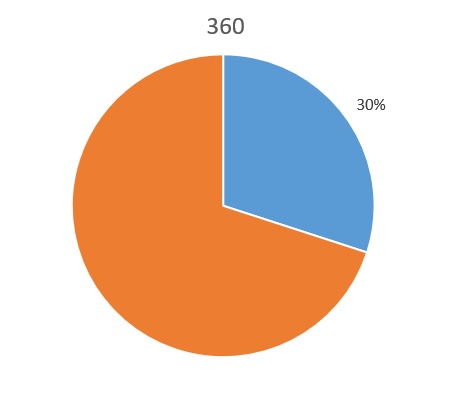
Como hemos visto 30% significa 30 de cada 100, es una forma de dar la fracción \(\normalsize \frac{30}{100}\). Tendré que encontrar la otra fracción que es equivalente a esta. Como en esta tengo 30 de cada 100 el total es 100, ¿qué conozco en la otra fracción? El total también, solo que esta vez vale 360, así que lo que desconozco en esta ocasión es el numerador: \(\normalsize \frac{x}{360}\).
Las fracciones equivalentes en esta ocasión son:
\(\huge \frac{30}{100}=\frac{x}{360}\)
Por equivalencia de fracciones:
\(\large 100·x=30·360\)
Que conduce a que
\(\large x=108\)
El 30% de 360 es 108.
Regla de tres para calcular una cantidad conociendo un porcentaje de ella
Por ejemplo, sabemos que el 25% de una cantidad es 49. ¿Cuál es esa cantidad?
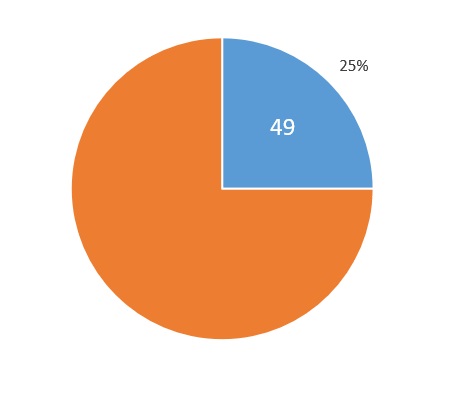
El 25% nos da la primera fracción, en la segunda conocemos el numerador, y no sabemos cuánto vale el denominador:
\(\huge \frac{25}{100}=\frac{49}{x}\)
Por equivalencia de fracciones:
\(\large 25·x=49·100\)
Que conduce a que
\(\large x=\frac{49·100}{25}=196\)
La cantidad que buscamos es 196.
Regla de tres para calcular el porcentaje de una cantidad desconocida sabiendo otro porcentaje de esa cantidad
Sabemos que 40% de una cantidad es 78, ¿cuánto será el 60% de esa misma cantidad?
Este caso es un poco diferente, porque venimos aplicando partes en el numerador y totales en el denominador, pero nada nos obliga a hacerlo siempre así, en realidad podemos perfectamente establecer relaciones como la que se ve a continuación, si el 40% es 78 y queremos calcular el 60%, podemos decir que esa cantidad valdrá X :
40 —— 78
60 —— X
Que se puede colocar como este par de fracciones equivalentes:
\(\huge \frac{40}{60}=\frac{78}{x}\)
\(\large 40·x=60·78\)
\(\large x=\frac{60·78}{40}=117\)
El 60% de esa cantidad es 117.
Regla de tres online
Ya hemos visto, con varios ejemplos, que calcular porcentajes apoyándonos en la regla de tres y la proporcionalidad no es nada difícil, no obstante, por si los números se complican y no tienes una calculadora a mano, te dejamos esta calculadora de porcentajes y regla de tres online.
Hoy hemos aprendido a solucionar diferentes problemas relacionados con porcentajes utilizando una misma herramienta: la regla de tres. Para conocer más sobre este y otros contenidos de matemáticas de primaria, regístrate en Smartick y pruébalo gratis.
Para seguir aprendiendo:
- Clasificación de fracciones: propias, impropias y unitarias
- Fracciones equivalentes: qué son y cómo calcularlas
- Ejercicios con fracciones equivalentes
- Resta de fracciones con ejercicios y ejemplos
- División de fracciones. Diferentes métodos
Técnico Superior en Administración y Finanzas, Quiromasajista, Masajista Deportivo y Músico.
Forma parte del equipo de desarrollo de contenidos de Smartick.
Curioso por naturaleza, música y ciencia son dos de sus pasiones.
- Características de la práctica significativa - 23/03/2020
- Cómo representar fracciones en la recta numérica - 10/02/2020
- Diagramas de Venn en Smartick - 13/01/2020
Gracias por el aporte, me sirvió bastante, saludos a todos.
Es muy bueno me ayudó mucho
Me sirvió de entendí a la perfección
Está bien
Hola me ayudó mucho a comprender mi tarea
Me ayudó mucho con un ejemplo para mi tarea ya que no podemos contar con los profesores por la pandemia ya que no pueden explicarnos
Esto me sirvió demasiado
Excelentes explicaciones, el cálculo del % en todas sus expreiones más básicas, los felicito en verdad, buen trabajo.
Smartick ayuda bastante, gracias y un saludo, gracias a Smartick mi hijo ha sacado un 10.
¡Nos alegramos por ese 10, Rede! En Smartick ofrecemos un montón de recursos para fomentar el conocimiento de nuestros alumnos. A parte de este blog, contamos con un método online de matemáticas personalizado que se adapta a las necesidades de cada alumno. Podéis disfrutar de nuestro periodo de prueba gratuito en nuestra página web https://www.smartick.es
¡Un saludo!
Son muy buenos resultados gracias a que enseñan muy bien, les agradezco Smartick
Nos alegramos de que te guste Sofía 😊
Muchas gracias por la ayuda me ha gustado mucho, besos.
¡Buen aporte! práctico para fijar el conocimiento indispensable: ¡felicidades!
Me ayudó, muchas gracias.
Muchas gracias Adrianzen, nos alegramos mucho de que el blog de Smartick te ayude.
¡Un saludo!