En el post de hoy vamos a repasar las restas en vertical. Como siempre, vamos a hacerlo con ejemplos que nos ayuden a entender mejor en qué consisten y cómo se realizan las restas en vertical.
Antes de empezar, vamos a repasar el material que utilizaremos para hacer las restas. ¿Cómo representamos un número con este material? ¡Muy fácil! Utilizaremos tantas unidades como corresponden al número, por ejemplo:
Y ¿para qué sirven las decenas? Para que sea más fácil representarla y no tengamos que utilizar unidades sueltas, las agrupamos en una barra que contiene 10 unidades:
Además, hoy vamos a hacer restas que incluyen centenas. Para representar mejor una centena, utilizaremos una placa de 100 unidades (que contiene 10 barras de 10 unidades cada una). Por ejemplo:
Restas en vertical
Vamos a empezar a ver las restas en vertical. Para entenderlo mejor, vamos a resolver dos restas:
328 – 124
647 – 15
Vamos a comenzar con la primera. Veremos dos pasos: el primero consiste en colocar los términos de la resta y el segundo en hacer la resta.
1. Colocamos los términos
Para hacer una resta en vertical debemos asegurarnos de que hemos colocado correctamente sus términos. Para ello, debemos colocar en la línea de arriba el minuendo y justo debajo, el sustraendo. Cuando los colocamos, debemos alinear en la misma columna las unidades con las unidades, las decenas con las decenas, etc:
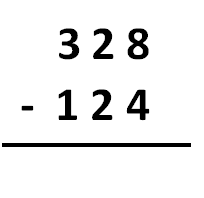
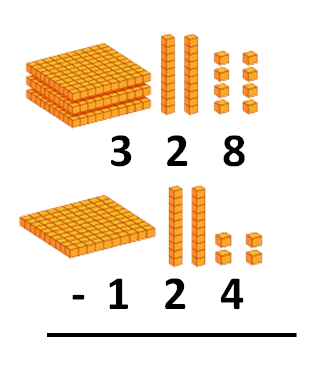
Para entender mejor cómo es, vamos a utilizar el material:
2. Hacemos la resta
Ahora tenemos que hacer la resta, teniendo en cuenta dos cosas muy importantes:
a) Siempre vamos a restar los números que hay en una misma columna
b) Empezamos por la columna de las unidades, y vamos avanzando por columnas hacia la izquierda
Así, primero restamos la columna de las unidades:
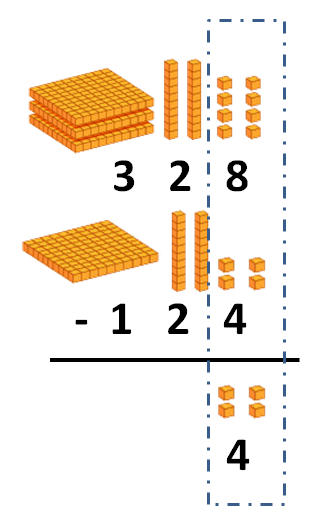
Y después la columna de las decenas:
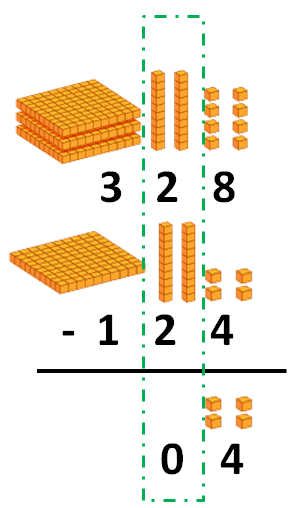
Y por último la columna de las centenas:
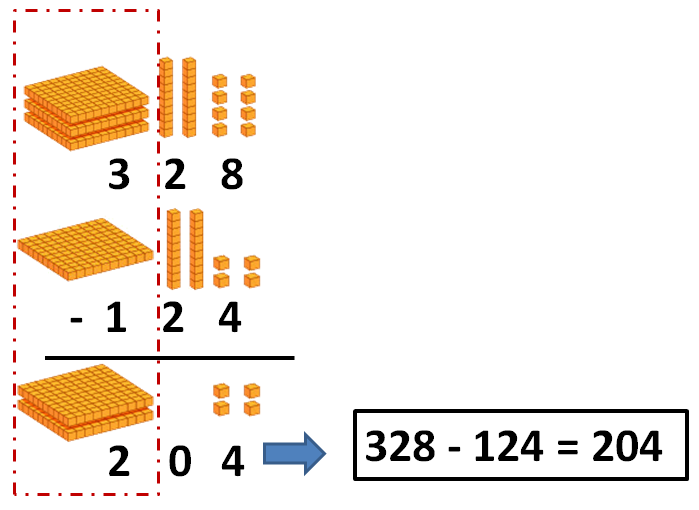
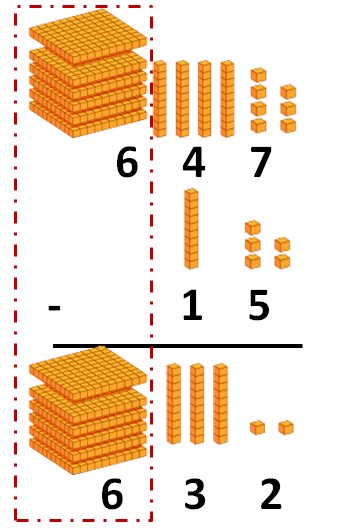
Y ¿qué pasa cuando en alguna columna no hay número? Pues hacemos lo mismo que antes: colocamos los términos desde la columna de las unidades hacia la izquierda, y restamos por columnas, empezando por las unidades. Para verlo mejor, vamos a resolver la segunda resta: 647 – 15
Primero la colocamos como hemos aprendido, y empezamos a restar por la columna de las unidades:
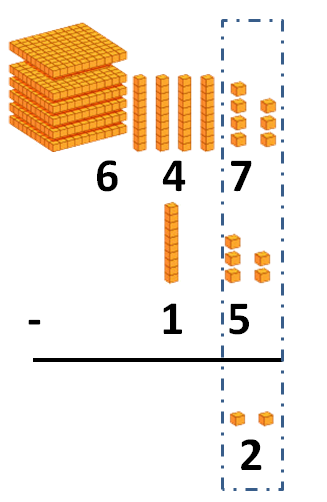
Y después la de las decenas:
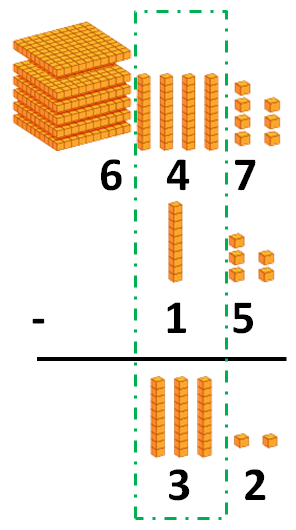
Por último, restamos en la columna de las centenas. Como el sustraendo tiene 0 centenas, el número de centenas sigue siendo el mismo:
Y… ¿Qué pasa si cuando vamos a restar los números de una columna el número de arriba es más pequeño que el de abajo? Si nos ocurre eso, debemos utilizar la llevada. Si quieres ver cómo se resuelve una resta con llevada con este mismo material, ve al siguiente enlace:
Ver post: Cómo resolver una resta con llevada
Y esto ha sido todo por hoy. ¿Qué te ha parecido este post? ¿Te ha ayudado a entender mejor cómo se hacen las restas en vertical?
Si quieres practicar restas en vertical, haz clic sobre los siguientes enlaces:
Practica ejercicios de restas en vertical sin llevada
Practica ejercicios de restas en vertical con llevada nivel 1
Practica ejercicios de restas en vertical con llevada nivel 2
Y recuerda que para seguir aprendiendo, puedes registrarte y probar Smartick gratis.
Para seguir aprendiendo:
- Repaso de sumas en vertical con varios ejemplos
- Aprender a restar con llevada
- Cómo resolver sumas sin llevadas
- Cómo resolver una resta con llevada
- Algoritmo de la suma. Suma en vertical con llevadas
Forma parte del equipo de desarrollo de contenidos de Smartick y se encarga de la elaboración y secuenciación de enunciados.
- Problemas con medidas de tiempo - 27/07/2015
- Líneas rectas, segmento y líneas semirrectas - 29/06/2015
- Problemas de división con decimales - 25/05/2015
Me preocupa mucho que este tipo de orientaciones para hacer restas impacte mucho en los docentes. No están bien enfocadas, verán las razones;
Si tengo 647 euros y una amiga me pide prestado 16 euros, será necesario que yo tenga los 647, ella los 15 y por otro lado los 632 de la diferencia?
Aquí hay un apego exagerado a lo formal desde lo concreto. Grave error.
Lo que sucede en la realidad es que tengo mis 647 euros (en el bolsillo), saco los 15 que me piden prestado y me quedan 632. No son necesarios más representaciones
¡Hola Elvis, muchas gracias por tu comentario y por compartir tus inquietudes! Es una reflexión interesante.
Si bien es cierto que este tipo de representaciones se escapan de un contexto real, constituyen un apoyo puntual que puede facilitar la comprensión del proceso, especialmente en la descomposición en unidades y al restar con llevadas. Al tratarse de un material manipulativo, los bloques de base diez ofrecen un nivel de concreción ideal para un estadio inicial. Y en caso de realmente tenerlos, pueden manipulase de manera similar a “ los euros en el bolsillo”. Se parte de una cantidad inicial y se van “quitando – sacando elementos”, no es indispensable tener representados el minuendo, el sustraendo y la diferencia por separado.
Entendemos tu preocupación y lejos de querer presentarlo como un método único, excluyente y permanente, pretendemos que sea un recurso adicional complementario a muchas otras experiencias y que, como cualquier otra representación, el alumno pueda prescindir de ella a medida que consigue abstracción, transferencia y generalización del aprendizaje.