Hoy vamos a aprender suma y resta con el método Singapur.
¿Qué es el Método Singapur?
Singapur es un pequeño país de Asia que en el año 1965 se encontró en una situación complicada: alto desempleo y analfabetismo. Eso hizo que los esfuerzos se centraran en la aplicación de un sistema educativo que se adaptara a las necesidades de crecimiento rápido. En los años 90 el mundo comenzó a avanzar más rápido y era necesario preparar a los alumnos para ese nuevo mundo, ya no solo a ser buenos profesionales, sino a ser personas capaces de aprender y reaprender haciendo frente a las nuevas situaciones. Ahí fue cuando nació el Método Singapur, tanto para las matemáticas como para las ciencias.
Un Método de aprendizaje que permite descubrir y potenciar las habilidades particulares de cada niño.
Bases del Método Singapur
El Método Singapur permite una aproximación significativa a las matemáticas, donde los niños se relacionan primero con elementos manipulativos concretos y luego con elementos prácticos de representación de los problemas. Cuando los niños ya se han familiarizado con los conceptos, avanzan usando representaciones abstractas tales como números, notaciones y símbolos.
Ahora que ya sabemos qué es el Método Singapur, vamos a pasar a ver cómo aprender a sumar y restar:
Barras de Singapur aplicadas a la suma
Claudia tiene 8 ositos de goma. Sergio tiene 6 ositos de goma. ¿Cuántos ositos de goma tienen entre los dos?
- En un primer momento los niños utilizan objetos concretos (o dibujos) para formar los dos grupos de ositos de goma, y luego unen los dos grupos.
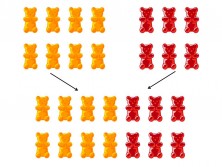
- Ahora pasamos de lo concreto, los ositos de goma, a lo pictórico: Las barras de Singapur. Donde es recomendable mantener algunas características de los objetos concretos, como por ejemplo los colores y las partes. En este caso hemos puesto los 8 ositos naranjas de Claudia en ocho partes de la barra de color naranja, y lo mismo hemos hecho con los 6 de Sergio.
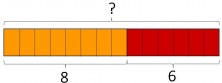
- Es interesante poder ver las barras como un todo comprendido en dos partes. El objetivo es unir las dos partes para encontrar el todo. La suma de dos grupos, objetos, dos cosas, etc…
- Una vez conocemos el resultado visualmente, pasamos a lo abstracto:
Parte + Parte = Todo
8 + 6 = 14
Solución: Tienen 14 ositos de goma entre los dos.
Barras de Singapur aplicadas a la resta
Tenemos 2 caramelos más que gominolas. Si hay 6 caramelos, ¿cuántas gominolas tenemos?
- En primer lugar los niños deben hacer una comparación. Utilizando objetos concretos (o dibujos), se colocan uno por uno los objetos para poder comparar sus cantidades:
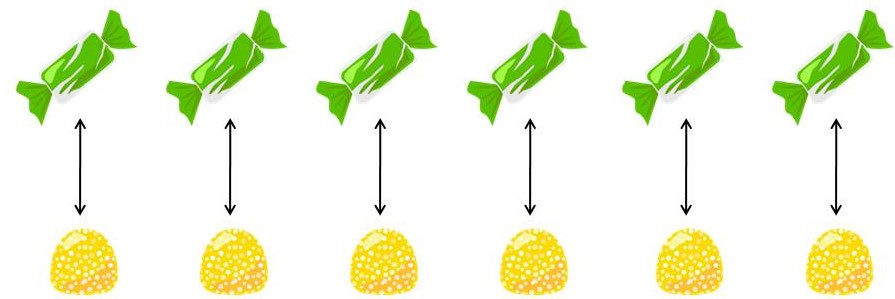Tenemos 6 caramelos. Hay tantos caramelos como gominolas, las dos cantidades son iguales.
- El paso intermedio entre lo concreto y lo pictórico es muy importante para visualizar la diferencia:
Tenemos 6 caramelos. Hay dos caramelos más que gominolas.
- Pasamos de lo concreto a lo pictórico. Modelo de comparación:
- Una vez conocemos el resultado visualmente, pasamos a lo abstracto:
Cantidad mayor – Diferencia = Cantidad menor
6 – 2 = 4
Solución: Hay 4 gominolas.
Este es el aprendizaje de la suma y resta con las Barras de Singapur.
Espero que os haya gustado y sobre todo que os sirva para entender mucho mejor el concepto de suma y resta.
En Smartick consideramos que el Método de Singapur, en concreto las barras de Singapur, es una herramienta muy interesante para la comprensión de las operaciones matemáticas.
Para seguir aprendiendo:
- Barras de Singapur aplicadas a la suma de fracciones
- Barras de Singapur aplicadas a la resolución de problemas II
- ¿Qué es un número?
- Barras de Singapur aplicadas a la resolución de problemas
- Fracción: aprende todo sobre fracciones
Mi profesión es totalmente vocacional, he trabajado en escuelas de educación libre en Madrid y fuera de España en proyectos de educación en India y Nicaragua.
Mi pasión son los niños y viajar a países de culturas muy diferentes.
- Barras de Singapur aplicadas al concepto de porcentaje - 07/08/2017
- Geometría y figuras planas con la ayuda del Tangram - 10/07/2017
- Qué es una división. Conceptos basicos - 12/06/2017
Super, me ha servido mucho para guiar a mi alumna durante las clases virtuales. Mil gracias. Saludos
Me parece genial es como estar jugando.
interesante el método
Práctica de matemática de los números enteros con método Singapur. Excelente, sigan
adelante con otros temas, más éxitos saludos y felicitaciones.
Estimada Ana,
Muchas gracias por siempre compartir tus experiencias sobre educación y sobre todo en estos métodos tan innovadores.
Un cordial saludo y éxitos.
Joel