Hoy vamos a resolver ejercicios de sumas y restas incompletas utilizando varias estrategias diferentes.
En matemáticas es importante saber utilizar estrategias diversas para resolver un mismo problema o ejercicio. Conocer varias estrategias, saber aplicarlas, y saber también cuándo es mejor aplicar cada una, es lo que llamamos «flexibilidad matemática». Para desarrollar el pensamiento matemático, la flexibilidad es fundamental.
Verás que es fácil resolver ejercicios de completar igualdades con sumas y restas. Intentaremos mostrarte lo importante que es afrontar estos ejercicios con la ayuda de la flexibilidad matemática.
Primer ejercicio de sumas y restas incompletas
Queremos completar la siguiente igualdad:
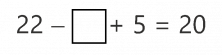
Una primera opción es operar los números para simplificar el ejercicio. Podemos cambiar el orden de las operaciones y sumar primero 22 + 5. Como sabemos que 22 + 5 = 27, nos quedaría resolver
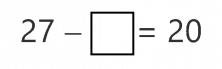
Esta igualdad es mucho más fácil, pues sabemos que solo hay que quitar 7 a 27 para tener 20. Así, siempre que podamos hacer alguna operación para simplificar un ejercicio, avanzaremos mucho.
Otra opción para resolver el ejercicio es utilizar el tanteo con números sencillos. Por ejemplo, si ponemos en la casilla vacía un 10, tenemos que 22 – 10 + 5 = 17.
No hemos dado con el resultado esperado, pero nos hemos acercado mucho. Hemos quitado 10 y el resultado nos ha dado menor de lo que deseábamos, 17 en vez de 20. Así que tendremos que quitar menos de 10, para que el resultado sea mayor. En lugar de 10, quitamos 7, porque nos habíamos equivocado por 3. Y ahora comprobamos el resultado:
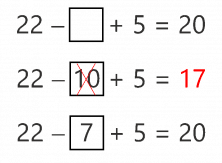
Segundo ejercicio de sumas y restas incompletas
Vamos a ver ahora otro ejemplo de sumas y restas incompletas. Par ello, intentaremos completar la siguiente igualdad:
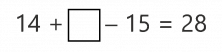
Para resolver algunas igualdades de este tipo está bien utilizar relaciones numéricas sencillas que ya conocemos. Por ejemplo, al ver el 14 y el 28, seguro que se te ocurre que 14 + 14 = 28. Parece que, si ponemos 14 en la casilla a rellenar, estaríamos muy cerca de 28 pero… ¡Después hay que restar 15! ¿Qué podemos hacer? Pues la solución sería poner 14 en la caja, para llegar a 28, y 15 más para compensar que después vamos a quitar 15. Al final, nos damos cuenta de que sumando 14 + 15 = 29 conseguimos nuestro objetivo.
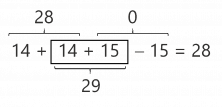
También podemos simplificar la igualdad. Para ello, antes, cambiamos el orden de las operaciones. Al número de la casilla, le vamos a tener que sumar 14 y restar 15. Pero sumar a un número primero 14 y luego restarle 15 es lo mismo que quitarle una unidad.
Si pensamos así, veremos que solo tenemos que encontrar un número al que, quitando 1, nos dé 28 y… ¡eso es tan fácil de hacer!
Volvemos a ver que hacer operaciones, u organizar los cálculos de otra forma, nos puede ayudar a convertir un ejercicio en otro mucho más sencillo.
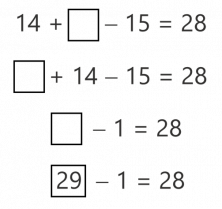
Esperamos que las ideas que te hemos dado en esta entrada te orienten para resolver otros ejercicios de sumas y restas incompletas y, sobre todo, estimulen el desarrollo de tu flexibilidad matemática. A partir de ahora, cuando te encuentres un ejercicio, pregúntate si puedes hacerlo de varias formas y cuál sería la más sencilla de ellas. Nunca pienses que hay una sola forma de resolver un problema o que, si lo resuelves “pensando a tu manera”, no va a ser válida tu respuesta. Siempre tiene un gran valor que desarrolles tus propias estrategias para pensar los problemas de matemáticas.
En nuestras sesiones diarias de matemáticas en Smartick nos esforzamos en enseñar diferentes estrategias para resolver cada contenido que presentamos. Si quieres conocer nuestro método, entra en Smartick y pruébalo gratis.
Para seguir aprendiendo:
- Estrategias para resolver sumas y restas en horizontal incompletas
- Operaciones combinadas con ejemplos resueltos
- Sumas y restas en horizontal. Cálculo mental
- Trucos para resolver operaciones combinadas
- Completar sumas, restas, multiplicaciones y divisiones
Fundador de la revista Edma 0-6: Educación Matemática en la Infancia. Miembro de la SEIEM.
Entusiasmado por la Educación Matemática en los primeros años. Cambiar la Educación Matemática es posible.
hola voy a aprender en Smartick
Me parece muy buena página para aprender mas cada día
Buen trabajo que nos ayuda mucho con los estudiantes .. felicitaciones
gracias por todo aunque ya lo había aprendido era necesario