En este post vamos a seguir analizando el libro de Craig Barton How I Wish I’d Taught Maths sobre la educación basada en evidencias. Hoy hablaremos del capítulo centrado en la auto explicación, es decir, las reflexiones que se hace uno mismo cuando está leyendo o aprendiendo algo.
Efectos de la auto explicación
La auto explicación consiste en dar sentido a lo que se está leyendo o aprendiendo. No tiene nada que ver con dar explicaciones a otros y no implica decir nada en alto. Consiste en parar, reflexionar un paso concreto de una solución y preguntarte a ti mismo: ¿qué significa el resultado que acabo de obtener? ¿cuál es el siguiente paso que debo dar?
Chi (2000) identificó dos efectos importantes al aplicar este tipo de prácticas en el aprendizaje de los alumnos:
- Generar inferencias. Los alumnos son capaces de encontrar información que no se facilita explícitamente.
- Reparar modelos incorrectos. A través de este tipo de procesos, lo alumnos son capaces de encontrar divergencias entre su modelo mental y el modelo transmitido por la solución.
Sin embargo, los estudiantes no hacen este tipo de práctica de forma natural y, por lo tanto, es necesario incitarles a que lo hagan.
En Smartick, una de las prácticas que realizamos para fomentar la creatividad y el razonamiento en la mente de los niños es a través de la resolución de problemas matemáticos. Gran parte de los problemas matemáticos que tenemos incorporados en el método no consisten únicamente en encontrar una solución cuantitativa.
Por ejemplo:
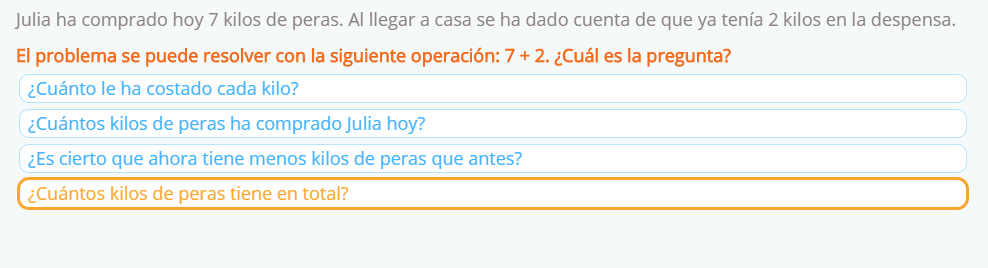
Este tipo de problemas ayudan a reparar estrategias incorrectas de resolución, como es el uso de palabras clave para determinar cuál es la operación correcta. Además, para resolverlos, los alumnos tienen que inferir información que no está explícitamente en el enunciado.
Prácticas para optimizar las auto explicaciones
-
Explicar si algo es correcto o incorrecto
Otra de las prácticas, según Craig Barton, para hacer que las auto explicaciones sean lo más efectivas posibles es explicar si algo es correcto o incorrecto.
Los ejemplos incorrectos deben utilizarse con cautela, pues pueden provocar que el alumno fije el error. Sin embargo, el resultado clave de Siegler’s (2002) es que «explicar por qué las respuestas correctas son correctas y las incorrectas son incorrectas produce un mayor aprendizaje que explicar solo por qué las repuestas correctas son correctas».
En Smartick, tenemos diseñadas tareas de evaluación que, más allá de juzgar la corrección o incorrección de una sentencia aritmética mediante un cálculo, se espera que conduzcan a los alumnos a juzgar la corrección o incorrección en términos estructurales (algebraicos).
Por ejemplo, utilizando su conocimiento informal de las propiedades de las operaciones (conmutativa, asociativa, elemento neutro, etc.):
Efectivamente al implementar este tipo de tareas y analizar los datos de efectividad, detectamos una dificultad a pesar de que no figuraban en las más difíciles en nuestras predicciones iniciales.
-
Auto explicación vs práctica
Una vez que nos hemos convencido de la importancia de la auto explicación, surge una pregunta bastante obvia:
¿Cuánto tiempo debemos dedicar a la auto explicación en relación a la práctica?
McEldoon et al (2013) intentó responder a esta pregunta. Los autores compararon la eficacia de la auto explicación con respecto a la eficacia de poner más práctica en problemas de primaria. Los estudiantes se dividieron en tres grupos. En el primer grupo resolvieron seis problemas y luego se les incitó a hacer una auto explicación. En el segundo grupo (el grupo de control) resolvieron seis problemas y no fueron incitados a hacer una auto explicación. Por último, el tercer grupo resolvió doce problemas y no fueron incitados a realizar una auto explicación. Los autores encontraron que en relación con el grupo de control los alumnos del primer grupo tenían mayor comprensión conceptual y fluidez.
Sin embargo, en relación con el grupo sometido a mayor práctica, el grupo 1 tiene beneficios, pero modestos. Los resultados sugieren que es necesario un equilibrio, tener en cuenta que las auto explicaciones no deben consumir todo el tiempo. La pausa para reflexionar sobre un resultado o un paso no debe durar más de unos segundos. No hace falta verbalizar la reflexión o discutirla. Los beneficios de las auto explicaciones se observan siempre que nos permitan seguir dedicando tiempo a la práctica.
Referencias:
- Chi, M. T. H. (2000), ‘Self-explaining: The dual processes of generating inference and repairing mental models in Claser, R. (ed.) Advance in instructional psychology: educational design and cognitive science, Vol. 5. Mahwah, NJ: Lawrence Erlbaum Associates, pp. 161-238
- Siegler, R. S. (2002) ‘Microgenetic studies of self-explanation’ in Granott, N. and Parziale, J. (eds) Microdevelopment: transition processes in development and learning. Cambridge Univertiy Press, pp. 31-35
- McEldoon, K. L., Durkin, K. L. nd Rittle-Johnson, B. (2013) ‘Is self-explanation worth the time? A comparison to additional practice’, British Journal of Educational Psychology 83 (4) pp. 615-632
- José Antonio Fernández Bravo, ‘La resolución de problemas matemáticos’
- Marta Molina González, ‘Desarrollo de pensamiento relacional y comprensión del signo del igual por alumnos de tercero de primaria’
Para seguir aprendiendo:
- «Todo pasa por algo” ¿Por qué creen los niños que ocurren las cosas?
- Ejemplos resueltos enriquecidos y metacognición
- El aprendizaje basado en problemas
- ¿Existe relación entre la auto regulación y la salud?
- Number talks: Aprende matemáticas hablando
Forma parte del equipo de desarrollo de contenidos de Smartick y se encarga de la elaboración y secuenciación de las actividades.
Amante de la meditación y con muchas ganas de cambiar la percepción que los niños tienen sobre las matemáticas.
- Resolución de problemas de matemáticas - 24/02/2020
- Las cinco etapas de la práctica deliberada - 06/01/2020
- La auto explicación en el proceso de aprendizaje - 25/11/2019