En este post vamos a continuar analizando el libro How I Wish I’d Taught Maths de Craig Barton sobre la educación basada en evidencias. Hoy nos centraremos en la resolución de problemas.
¿Qué es un problema?
Esta es la primera pregunta que debemos responder antes de abordar este tema.
Pongamos dos ejemplos.
- En un colegio hay 1000 estudiantes y 1000 casilleros. El primer día, la profesora le pide al primer estudiante que pase por todos ellos y los abra. Al segundo le pide que pase por ellos de dos en dos y cierre los que estén abiertos. Al tercero, que pase por ellos de tres en tres y cierre los que están abiertos y abra los que están cerrados. Al cuarto le pide lo mismo que al resto, pero le dice que lo haga de cuatro en cuatro… El proceso se termina cuando todos los estudiantes pasan por el pasillo abriendo y cerrando casilleros. ¿Cuántos casilleros están abiertos al final?
- Una chaqueta cuesta 52 euros y tiene un 20% de descuento, ¿cuánto costaba la chaqueta antes del descuento?
Es bastante evidente que el primero es un problema, sin embargo ¿lo es también el segundo?
Schoenfeld (2009) establece dos definiciones diferentes de problemas verbales:
- Cualquier cosa que tiene que ser resuelta.
- Una pregunta que te haga pensar, confusa o complicada.
Estrategias de resolución
Partiendo del modelo de Dewey, en el que se describen etapas del pensamiento en la resolución de problemas, los primeros trabajos de Polya estudian el empleo de estrategias heurísticas en la resolución de problemas matemáticos, proponiendo una colección de indicaciones, preguntas y sugerencias para ayudar a los estudiantes en su resolución.
Estas indicaciones se agrupan en 4 fases: comprender el problema, desarrollar una estrategia, ejecutar el plan y examinar la solución obtenida.
Parece sensato asumir que para tener éxito en la resolución de problemas un estudiante deba ser capaz de seguir estas cuatro fases.
Sin embargo, esta suposición merece un examen más detenido, especialmente dada la dificultad de muchos estudiantes en atravesar las etapas. Además, trabajos en posteriores de Schoenfeld (1992) concluyen que el uso de estrategias heurísticas no resulta exitoso y recomienda desarrollar estrategias para problemas específicos.
Por ejemplo, hagamos un breve análisis sobre la segunda fase: desarrollar una estrategia. Es fácil darse cuenta, si cogemos un examen cualquiera de matemáticas, que no podemos aprender estrategias generales de resolución para todos los problemas que aparecen. Es más, no podemos enseñar tales estrategias en ausencia de un conocimiento específico de la materia.
Dentro de esta segunda fase encontramos consejos como encontrar un patrón, hacer una lista, realizar un dibujo, eliminar posibilidades, usar un modelo, considerar casos especiales, trabajar hacia atrás o usar una fórmula.
Este tipo de consejos, como por ejemplo hacer un dibujo, es algo que efectivamente puede ayudar a los estudiantes a centrarse en la estructura profunda de toda una serie de problemas. Pero para poder realizar un diagrama correcto, los estudiantes deben ser capaces de incorporar en el diagrama las características claves del problema.
Modelos de fases en Smartick
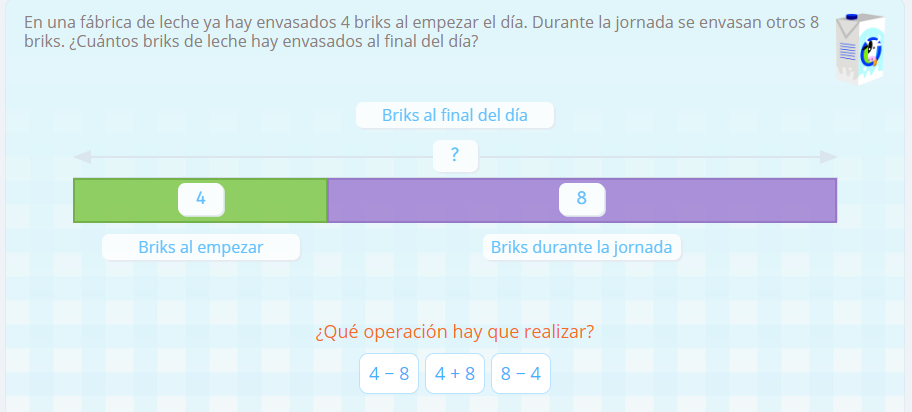
En Smartick tampoco trabajamos estrategias heurísticas generales. Nuestro modelo de fases para la resolución de problemas descansa en estrategias ligadas al contenido concreto. Nos basamos en el método Singapur para dar pautas específicas sobre la naturaleza del problema.
Referencias:
- Shoenfeld, A. (2009), ‘Learning to think mathematically: problem solving, metacognition, and sense-making in mathematics’ in Grouws, D. (ed.) Handkbook for research on mathematics teaching and learning.
- Polya, G. (1945) How to solve it
Para seguir aprendiendo:
- ¡Houston, tenemos un problema!
- Marco teórico del Método Singapur
- Singapur: Experiencias de aprendizaje
- Barras de Singapur aplicadas a la resolución de problemas II
- Barras de Singapur aplicadas a la resolución de ecuaciones algebraicas I
- Resolución de problemas de matemáticas - 24/02/2020
- Las cinco etapas de la práctica deliberada - 06/01/2020
- La auto explicación en el proceso de aprendizaje - 25/11/2019








Me encanta Smartick amo Smartick gracias
¡Vuestro método es simplemente fantástico!
Creo que no hay niño al que se le resista. Explicáis todo de una manera tan clara y amena que conseguís que nuestros hijos disfruten cada día más, dejando atrás las perezas y frustraciones.
es bueno
Es bueno