Hoy vamos a hablar de una herramienta que hemos introducido entre los recursos que apoyan el aprendizaje de los niños que haces sus sesiones diarias de Smartick Matemáticas: la doble recta numérica.
Índice
¿Qué es la doble recta numérica?
La doble recta numérica es una herramienta que nos ayuda a la hora de resolver problemas de proporcionalidad directa. Consiste en dos semirrectas puestas en paralelo. Como los problemas de proporcionalidad relacionan dos magnitudes, utilizamos cada una de las rectas para poner los datos que tenemos de esa magnitud a la misma altura.
¿Cómo se utiliza la doble recta numérica?
Como es posible que la explicación anterior te haya parecido confusa, te recomendamos que veas el siguiente vídeo de una actividad guiada de Smartick para que entiendas mejor cómo se utiliza.
Haciendo un paso a la unidad
En la práctica cualquiera que quiera resolver un problema de de proporcionalidad, tanto proporcionalidad directa como proporcionalidad inversa, puede hacerlo calculando primero lo que se llama el paso a la unidad, ¿en qué consiste? En el siguiente ejemplo de proporcionalidad directa en la doble recta numérica se ve muy claro.
Nos dan el precio de 4 neumáticos, en el primer paso calculamos el precio de un único neumático:
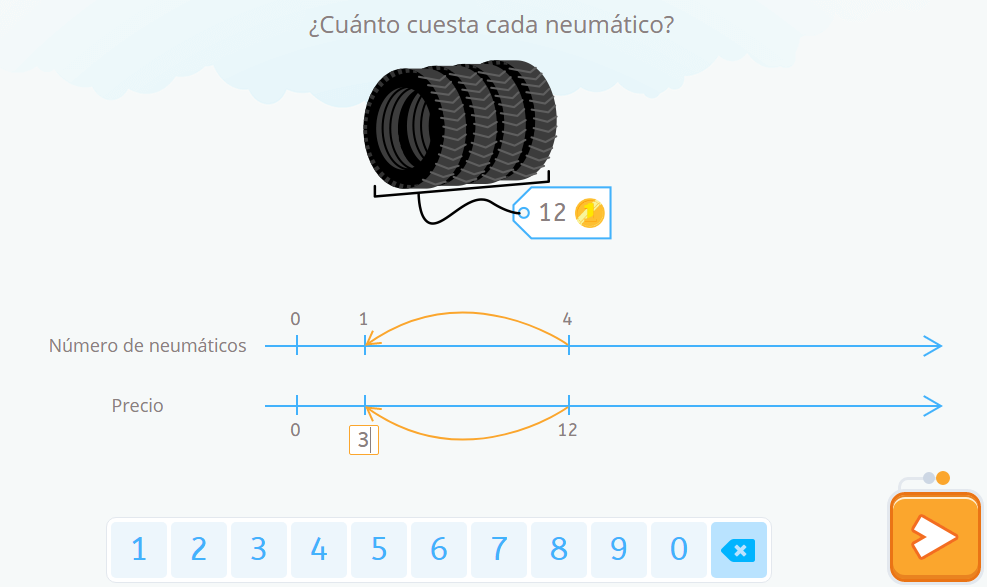
Una vez que sabemos y hemos representado en la doble recta numérica el precio de un neumático veremos que para calcular el precio de 6 solo necesitamos multiplicar por seis el precio de esa unidad:
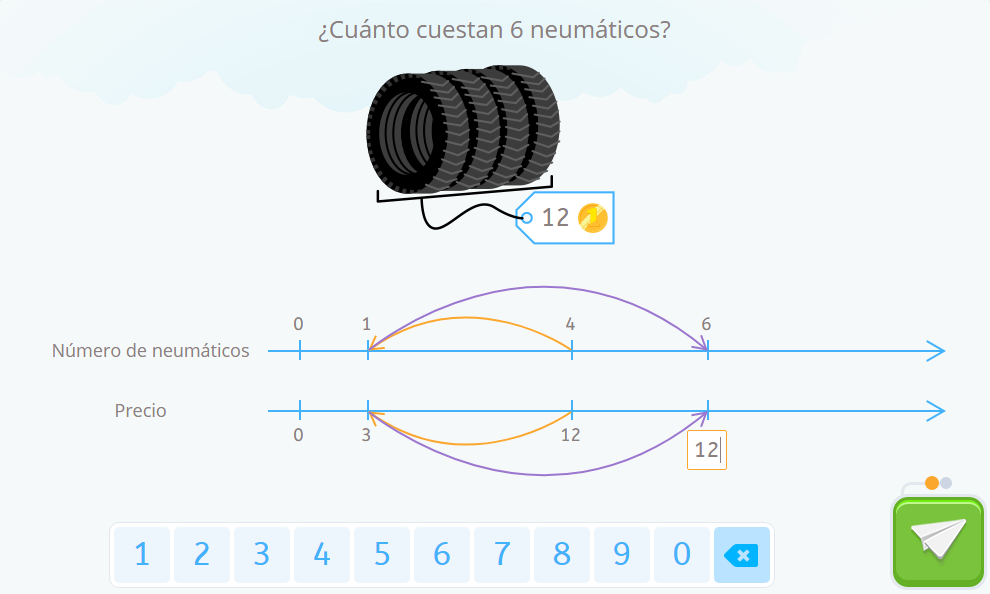
Utilizando la constante de proporcionalidad o razón
De una manera muy parecida, pero un poco más abstracta que la forma anterior, podemos directamente preguntarnos por el precio unitario como en el siguiente ejemplo:
Como seis tarrinas han costado 18 euros, cada tarrina cuesta 3 euros, 3 es el precio unitario, o constante de proporcionalidad en esta situación.
Si la pregunta ahora es por el precio de 3 tarrinas de helado, solo tendremos que multiplicar por esa constante de proporcionalidad para obtenerlo: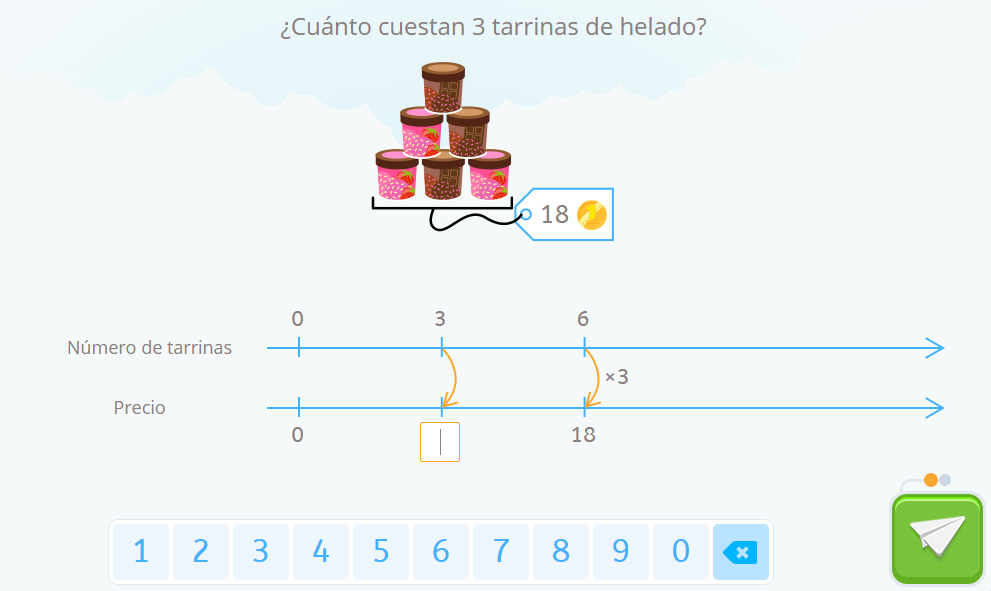 
¿En qué tipo de problemas se utiliza la doble recta numérica?
La doble recta numérica se utiliza en situaciones o problemas de proporcionalidad directa, cuando dos variables se relacionan de manera que las dos crecen o decrecen simultáneamente y en la misma proporción (si una se dobla, la otra también, si una se triplica, la otra también se triplica…). No es la única situación que puede darse, existe también la proporcionalidad inversa (cuando una magnitud de dobla, por ejemplo, la otra se reduce en la mitad…). Además hay situaciones que parecen de proporcionalidad… pero no lo son. Puedes ver ejemplos de problemas de proporcionalidad aquí.
¿Doble recta numérica o regla de tres?
Ha habido mucha polémica en las redes sociales recientemente sobre si se debía o no enseñar la «regla de tres» en la escuela. La regla de tres es de esos contenidos que, como adulto, se recuerdan como verdaderamente útiles de los muchos aprendidos en la escuela, y lo es, sobre todo a la hora de calcular descuentos o incrementos con porcentajes, algo que de adultos tenemos que hacer a menudo.
La regla de tres consiste en calcular un cuarto número a partir de 3 números que están en proporcionalidad. Lo que estamos haciendo con la doble recta numérica es calcular ese cuarto número, esa regla de tres, con la ayuda de un modelo (la doble recta) que nos permite confirmar que lo que tenemos delante es una proporcionalidad directa.
El principal problema de aprender procedimientos de cálculo sin comprensión (aquello del «este por este entre este» que se aplicaba en la regla de tres) es que si se nos presenta una situación de proporcionalidad inversa o de no proporcionalidad, y aplicamos una regla de tres sin comprender lo que estamos haciendo, acabaremos dando un resultado erróneo.
Para ilustrar mejor esto vamos a ver un ejemplo. Si nos dicen que tres pintores terminarán de pintar una casa en 6 días, y nos preguntan por el tiempo que tardarían 4 pintores. Suena proporcional y lo colocamos sin dudar en una regla de tres de las que hacíamos en el colegio de pequeños:
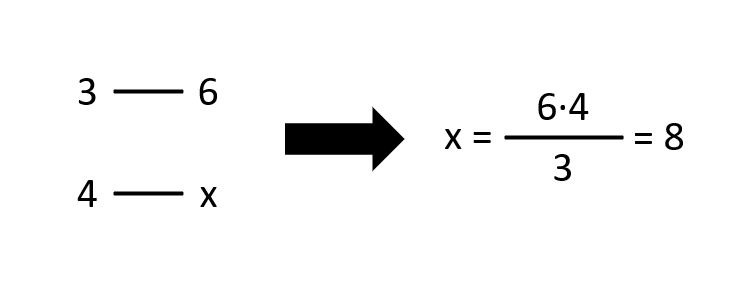
Solución: 8 días. Un momento, ¿no decían que tres pintores tardaban 6 días? ¿4 pintores tardan 8? El resultado de aplicar sin pensar la regla de tres es absurdo, porque si trabajan más pintores deberían tardar menos tiempo, es de hecho una típica situación de proporcionalidad inversa. Había que multiplicar el 6 por el 3 y dividir por 4, lo que también llamábamos «regla de tres inversa». También teníamos «reglas de tres» compuestas, en las que participaban más números, por ejemplo el de pintores, el de horas que trabajaban al día y el de días que tardaban en terminar…
El problema de aplicar sin comprensión la regla de tres es el que se suele ejemplificar con «el que tiene un martillo del cielo le caen los clavos». Tenemos un martillo, la regla de tres, que es muy efectivo en situaciones de porcentajes, descuentos e incrementos (todas de proporcionalidad directa) golpeamos con él a todo, como si fuesen clavos, y cuando estamos en situaciones que no son de proporcionalidad directa, seguimos utilizándolo.
Afrontar la proporcionalidad directa con una herramienta como la doble recta numérica nos lleva a una mayor comprensión de la proporcionalidad, con un modelo mental al que agarrarnos para poder juzgar si lo que tenemos delante es o no es proporcional y, si lo es, si es directo o inverso. Y así ir caminando con un poco más de certeza al cálculo de ese cuarto número a partir de tres dados, la regla de tres en un sentido amplio.
En resumen: en Smartick enseñamos la regla de tres, sí, pero con la doble recta numérica sirviendo de apoyo para los casos de proporcionalidad directa.
Regístrate en Smartick para probarlo de manera gratuita. Podrás practicar ejercicios y problemas de proporcionalidad y contenidos de matemáticas de primaria adaptados a tu nivel.
Bibliografía
Hay abundante evidencia científica sobre el uso de la doble recta numérica en enseñanza de la proporcionalidad directa. Si quieres consultar alguna de la que hemos valorado para introducir este contenido en Smartick, os dejamos estos enlaces:
Para seguir aprendiendo:
- Proporcionalidad inversa, regla de tres inversa
- Regla de 3: resumen de entradas
- Regla de 3 compuesta: cuándo se utiliza y algunos problemas
- Regla de 3 simple directa e inversa
- Problemas de proporcionalidad
Es formador de maestros, tanto en formación inicial en la Facultad de Educación de la Universidad Complutense de Madrid como en formación continuada. Apasionado de tocar las matemáticas.
Forma parte del equipo de Didáctica de Smartick.
Autor del blog Tocamates y del libro “Y me llevo una”.
Le encanta la divulgación y -en general- la comunicación. No calla ni debajo del agua, de ahí que colabore con varias radios y medios de comunicación, y que si tiene un rato, se eche unos largos en la piscina.
- El lenguaje de funciones y gráficas - 14/02/2024
- Cómo aplicar la jerarquía de operaciones - 20/09/2023
- Expresiones algebraicas: ¿Qué son? ¿Para qué sirven? - 21/07/2023